题目内容
14. 如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为mA=$\frac{1}{2}$mB=m,轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动.当轻杆转至水平位置时,A球速度为$\sqrt{\frac{2}{3}gl}$,则在以后的运动过程中( )
如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为mA=$\frac{1}{2}$mB=m,轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动.当轻杆转至水平位置时,A球速度为$\sqrt{\frac{2}{3}gl}$,则在以后的运动过程中( )| A. | A球机械能守恒 | |
| B. | 当B球运动至最低点时,球A对杆作用力等于0 | |
| C. | 当B球运动到最高点时,杆对B球作用力等于0 | |
| D. | A球从图示位置运动到最低点的过程中,杆对A球做功等于0 |
分析 题目中以O为支点时系统恰好平衡,说明是匀速圆周运动,根据向心力公式求解出需要的向心力,比较其与重力的关系来得出杆的弹力情况,结合动能定理分析弹力做功情况.
解答 解:A、由题意可知A、B组成的系统只有重力做功,机械能守恒,B球的机械能增大,则A球的机械能减小,故A错误;
B、以O为支点时系统力矩恰好平衡,说明是两球做匀速圆周运动;两个球的角速度相等,转动半径之比为2:1,根据v=rω,故两个球的线速度之比为2:1;
当A球运动至最高点时,B球运动至最低点,由于A球的向心力 F向=m$\frac{{v}^{2}}{\frac{2}{3}l}$=m$\frac{(\sqrt{\frac{2}{3}gl})^{2}}{\frac{2}{3}l}$=mg,由牛顿第二定律可知轻杆此时对球A作用力等于0,故B正确;
C、当B球运动到最高点时,B球的向心力F向=2m•$\frac{(\frac{v}{2})^{2}}{\frac{1}{3}l}$=2m•$\frac{(\frac{1}{2}\sqrt{\frac{2}{3}gl})^{2}}{\frac{1}{3}l}$=$\frac{1}{9}$mg<mBg;故杆对B球作用力为支持力;故C错误;
D、A球从图示位置运动到最低点的过程中,动能不变,重力做正功,故杆的弹力做等量的负功;故D错误;
故选:B.
点评 本题关键是知道两个球的机械能均不守恒,是两个球系统的机械能守恒,同时要结合向心力公式列式求解需要的向心力,比较其与重力的大小关系来判断有无弹力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图所示,小球A被长为L的细线悬于固定点O;B球被支架固定于O点的正下方,与O点的距离为h,A、B之间连有一劲度系数为K1的轻质弹簧,两小球均 处于静止状态,现将A、B间的弹簧换成一劲度系数为K2(K2>K1)的轻质弹簧,两小球重新静止后,细线AO的拉力大小将( )
处于静止状态,现将A、B间的弹簧换成一劲度系数为K2(K2>K1)的轻质弹簧,两小球重新静止后,细线AO的拉力大小将( )
 处于静止状态,现将A、B间的弹簧换成一劲度系数为K2(K2>K1)的轻质弹簧,两小球重新静止后,细线AO的拉力大小将( )
处于静止状态,现将A、B间的弹簧换成一劲度系数为K2(K2>K1)的轻质弹簧,两小球重新静止后,细线AO的拉力大小将( )| A. | 变大 | B. | 不变 | C. | 变小 | D. | 无法确定 |
2. 将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )
将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )
 将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )
将质量为m甲=1kg、m乙=0.5kg的甲、乙两根条形磁铁放在光滑水平面上,其N极相对,轴线在同一直线上.如图所示,现轻推以下使它们相向运动,某时刻它们的速度大小分别为V甲=2m/s,V乙=3m/s,方向如图,如果两磁铁没有接触就分开了,则以下判断中正确的是( )| A. | 甲反向时,乙的速度为1m/s,方向不变 | |
| B. | 乙反向时 甲的速度为0.5m/s,方向不变 | |
| C. | 甲、乙相距最近是速度均为零 | |
| D. | 甲、乙相距最近是速度均为$\frac{1}{3}$m/s |
9. 如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动,缸壁导热性良好使缸内气体的温度保持与外界大气温度相同,则下列结论中正确的是( )
如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动,缸壁导热性良好使缸内气体的温度保持与外界大气温度相同,则下列结论中正确的是( )
 如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动,缸壁导热性良好使缸内气体的温度保持与外界大气温度相同,则下列结论中正确的是( )
如图所示,一根竖直的弹簧支持着一倒立气缸的活塞,使气缸悬空而静止.设活塞与缸壁间无摩擦,可以在缸内自由移动,缸壁导热性良好使缸内气体的温度保持与外界大气温度相同,则下列结论中正确的是( )| A. | 若外界大气压增大,大气温度不变,则弹簧将压缩一些 | |
| B. | 若外界大气压增大,大气温度不变,则气缸的上底面距地面的高度将增大 | |
| C. | 若大气温度升高,外界大气压不变,则活塞距地面的高度将减小 | |
| D. | 若大气温度升高,外界大气压不变,则气缸的上底面距地面的高度将增大 |
6.一人用力踢质量为1kg的足球,使球由静止以10m/s的速度沿水平方向飞出,假设人踢球时对球的平均作用力为200N,球在水平方向运动了20m,那么人对球所做的功( )
| A. | 50J | B. | 200J | C. | 4000J | D. | 非上述各值 |
3. 如图所示,沿x轴正方向传播的一列简谐机械波在某时刻的波形图为一正弦曲线,其波速为100m/s,下列说法中正确的是( )
如图所示,沿x轴正方向传播的一列简谐机械波在某时刻的波形图为一正弦曲线,其波速为100m/s,下列说法中正确的是( )
 如图所示,沿x轴正方向传播的一列简谐机械波在某时刻的波形图为一正弦曲线,其波速为100m/s,下列说法中正确的是( )
如图所示,沿x轴正方向传播的一列简谐机械波在某时刻的波形图为一正弦曲线,其波速为100m/s,下列说法中正确的是( )| A. | 图示时刻后极短时间内质点b的加速度一定减小 | |
| B. | 从图示时刻开始,经过0.05s,质点a走过的路程为5m | |
| C. | 若此波遇到另一列波并发生稳定干涉现象,则另一列波的频率为25Hz | |
| D. | 若该波传播中遇到宽约4m的障碍物,则能发生明显的衍射现象 |





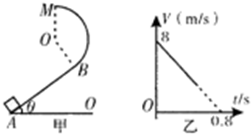 如图甲所示,一半径为R=1m,竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ,t=0时刻,有一质量m=2kg的物块从A点开始沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示.若物块恰能到达M点,求:
如图甲所示,一半径为R=1m,竖直圆弧形光滑轨道,与斜面相切于B处,圆弧轨道的最高点为M,斜面倾角θ,t=0时刻,有一质量m=2kg的物块从A点开始沿斜面上滑,其在斜面上运动的速度变化规律如图乙所示.若物块恰能到达M点,求: