题目内容
17.某同学在“探究小车速度随时间变化规律“实验中,由打点计时器得到表示小车运动过程的一条清晰纸带如图1所示,
(1)已知电火花式打点计时器所用交流电的频率为50Hz,纸带上各计数点的间距如图1,其中每相邻两点之间还有4个记录点未画出,计算小车运动加速度的表达式为a=$\frac{{(x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$.
(2)某同学量得x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.23cm.由此计算出打点计时器打下B、C、D、F时小车的瞬时速度,则打点计时器打下E点时小车的瞬时速度vD=0.864m/s,vE=0.928m/s(小数点后保留三位数字).
| 位置 | B | C | D | E | F |
| 速度(m•s-1) | 0.737 | 0.801 | 0.992 |
分析 (1)根据连续相等时间内的位移之差是一恒量,运用逐差法求出加速度.
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出D、E的瞬时速度.
(3)作出小车的速度时间图线,结合图线的斜率求出物体的加速度.
解答 解:(1)根据△x=aT2,运用逐差法得,a=$\frac{{(x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$.
(2)D点瞬时速度等于CE段的平均速度,${v}_{D}=\frac{{x}_{3}+{x}_{4}}{2T}$=$\frac{(8.33+8.95)×1{0}^{-2}}{0.2}$m/s=0.864m/s.E点的瞬时速度等于DF段的平均速度,则${v}_{E}=\frac{{x}_{4}+{x}_{5}}{2T}=\frac{(8.95+9.61)×1{0}^{-2}}{0.2}$m/s=0.928m/s.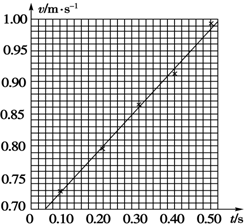
(3)小车的速度时间图线如图所示,图线的斜率表示加速度,a=$\frac{△v}{△t}=\frac{0.97-0.70}{0.46-0.04}≈0.64m/{s}^{2}$.
故答案为:(1)$\frac{{(x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$,(2)0.864,0.928,(3)0.64.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,主要是匀变速直线运动推论的运用.注意有效数字的保留.

练习册系列答案
相关题目
8.一质点做匀速直线运动,现对其施加一恒力,且原来作用在质点上的力不发生改变,则( )
| A. | 质点速度的方向总是与该恒力的方向相同 | |
| B. | 质点速度的方向总是与该恒力的方向垂直 | |
| C. | 质点加速度的方向与该恒力的方向不可能总是相同的 | |
| D. | 质点单位时间内速度的变化量总是不变的 |
12.关于加速度,下列说法正确的是( )
| A. | 加速度就是增加的速度 | |
| B. | 加速度是描述速度变化大小的物理量 | |
| C. | 加速度的方向和速度方向是相同的 | |
| D. | 加速度大表示速度变化快 |
2.今有甲、乙两个电阻,在相同时间内流过甲的电荷量是乙的2倍,甲、乙两端的电压之比为1:3,则甲、乙两个电阻阻值的比值为( )
| A. | 1:6 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
9.关于速度和加速度的方向,下列说法正确的是( )
| A. | 速度方向为正,加速度方向一定为正 | |
| B. | 速度的方向就是加速度的方向 | |
| C. | 速度改变量的方向就是加速度的方向 | |
| D. | 当加速度与速度方向相同且又减小时,物体做减速运动 |
7. 在某次发射科学实验卫星“双星”中,放置了一种磁强计,用于测定地磁场的磁感应强度.磁强计的原理如图所示(背面),电路中有一段金属导体,它的横截面是宽为a、高为b的长方形,放在沿y轴正方向的匀强磁场中,导体中通有沿x轴正方向、大小为I的电流.已知金属导体单位体积中的自由电子数为n,电子电荷量为e.金属导电过程中,自由电子做定向移动可视为匀速运动.测出金属导体前后两个侧面间的电势差为U.则下列说法正确的是( )
在某次发射科学实验卫星“双星”中,放置了一种磁强计,用于测定地磁场的磁感应强度.磁强计的原理如图所示(背面),电路中有一段金属导体,它的横截面是宽为a、高为b的长方形,放在沿y轴正方向的匀强磁场中,导体中通有沿x轴正方向、大小为I的电流.已知金属导体单位体积中的自由电子数为n,电子电荷量为e.金属导电过程中,自由电子做定向移动可视为匀速运动.测出金属导体前后两个侧面间的电势差为U.则下列说法正确的是( )
 在某次发射科学实验卫星“双星”中,放置了一种磁强计,用于测定地磁场的磁感应强度.磁强计的原理如图所示(背面),电路中有一段金属导体,它的横截面是宽为a、高为b的长方形,放在沿y轴正方向的匀强磁场中,导体中通有沿x轴正方向、大小为I的电流.已知金属导体单位体积中的自由电子数为n,电子电荷量为e.金属导电过程中,自由电子做定向移动可视为匀速运动.测出金属导体前后两个侧面间的电势差为U.则下列说法正确的是( )
在某次发射科学实验卫星“双星”中,放置了一种磁强计,用于测定地磁场的磁感应强度.磁强计的原理如图所示(背面),电路中有一段金属导体,它的横截面是宽为a、高为b的长方形,放在沿y轴正方向的匀强磁场中,导体中通有沿x轴正方向、大小为I的电流.已知金属导体单位体积中的自由电子数为n,电子电荷量为e.金属导电过程中,自由电子做定向移动可视为匀速运动.测出金属导体前后两个侧面间的电势差为U.则下列说法正确的是( )| A. | 电流方向沿x轴正方向,正电荷受力方向指向前侧面,因此前侧面电势较高 | |
| B. | 电流方向沿x轴正方向,电子受力方向指向前侧面,因此后侧面电势较高 | |
| C. | 磁感应强度的大小为B=$\frac{nebU}{I}$ | |
| D. | 磁感应强度的大小为B=$\frac{2nebU}{I}$ |


 如图所示,匀强磁场的方向垂直于纸面向里,P和Q是两个带电粒子在磁场中的运动径迹,图中箭头表示粒子的运动方向.那么,径迹为P的粒子的电性为正,径迹为Q的粒子的电性为负.(选填“正”或“负)
如图所示,匀强磁场的方向垂直于纸面向里,P和Q是两个带电粒子在磁场中的运动径迹,图中箭头表示粒子的运动方向.那么,径迹为P的粒子的电性为正,径迹为Q的粒子的电性为负.(选填“正”或“负)