题目内容
12.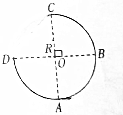 如图所示,半径为R的光滑的四分之三圆弧轨道竖直放置,A、C两点分别为轨道的最低点和最高点,一质量为m的小环套在轨道上,小环以水平向右的初速度从A出发经C点后,恰可撞击到D点.求:
如图所示,半径为R的光滑的四分之三圆弧轨道竖直放置,A、C两点分别为轨道的最低点和最高点,一质量为m的小环套在轨道上,小环以水平向右的初速度从A出发经C点后,恰可撞击到D点.求:(1)小环到达C点瞬间轨道对环的弹力的大小和方向;
(2)设小环撞击到D点后又能套在圆轨道上,那么相对A点能上升的最大高度是多少?
分析 (1)小环从C到D做平抛运动,根据高度求出平抛运动的时间,结合水平位移和时间求出小环通过C点时的速度.在C点,由牛顿第二定律求轨道对环的弹力.
(2)小环撞击D点后水平方向的分速度突然减至零,只剩竖直分速度,由平抛运动的规律求出竖直分速度,再由机械能守恒定律求小环相对A点能上升的最大高度.
解答 解:(1)小环从C到D做平抛运动,由平抛运动的规律有:
R=$\frac{1}{2}g{t}^{2}$
R=vCt
解得:vC=$\sqrt{\frac{1}{2}gR}$
在C点,以小环为研究对象,设轨道对小环的弹力方向竖直向上,大小为F.根据牛顿第二定律得:
mg-F=m$\frac{{v}_{C}^{2}}{R}$
解得:F=$\frac{1}{2}$mg
由于F>0,所以假设正确,即轨道对环的弹力的方向竖直向上.
(2)小环撞击D点后水平方向的分速度突然减至零,只剩竖直分速度,竖直分速度为:vy=gt=$\sqrt{2gR}$
设小环相对A点能上升的最大高度为h.取A点为参考点,根据机械能守恒定律得:
$\frac{1}{2}m{v}_{y}^{2}$+mgR=mgh
解得:h=2R
答:(1)小环到达C点瞬间轨道对环的弹力的大小是$\frac{1}{2}$mg,方向竖直向上;
(2)设小环撞击到D点后又能套在圆轨道上,那么相对A点能上升的最大高度是2R.
点评 本题考查了平抛运动、向心力与机械能守恒定律的综合,要知道平抛运动在水平方向和竖直方向上的运动规律,明确圆周运动向心力的来源:指向合外力.关键要判断出小环撞击D点时速度的变化.

练习册系列答案
相关题目
2. 由波源产生的一列简谐横波,沿x轴正方向传播,在t=0时刻的波形如图所示,质点P的x坐标为3m.已知波源在一分钟之内完成全振动75次.在x=40m处有一处于静止状态的接收器(图中没有画出),下列说法正确的是( )
由波源产生的一列简谐横波,沿x轴正方向传播,在t=0时刻的波形如图所示,质点P的x坐标为3m.已知波源在一分钟之内完成全振动75次.在x=40m处有一处于静止状态的接收器(图中没有画出),下列说法正确的是( )
 由波源产生的一列简谐横波,沿x轴正方向传播,在t=0时刻的波形如图所示,质点P的x坐标为3m.已知波源在一分钟之内完成全振动75次.在x=40m处有一处于静止状态的接收器(图中没有画出),下列说法正确的是( )
由波源产生的一列简谐横波,沿x轴正方向传播,在t=0时刻的波形如图所示,质点P的x坐标为3m.已知波源在一分钟之内完成全振动75次.在x=40m处有一处于静止状态的接收器(图中没有画出),下列说法正确的是( )| A. | 质点P的振动速度为5m/s | |
| B. | 横坐标为15m的质点在t=0.4s时恰好位于波峰 | |
| C. | t=0时刻开始,当质点P第一次位于平衡位置时,横坐标为17m的质点恰好位于波谷 | |
| D. | 若波源沿x轴正方向运动,接收器接收到的波的频率可能为0.25Hz |
20.某物体沿直线运动的速度-时间图象如图所示,从图象可以看出,下列选项中正确的是( )


| A. | 物体在做单向直线运动 | B. | 物体的加速度大小始终不变 | ||
| C. | 第3 s末时物体的加速度为零 | D. | 前6s内物体的位移为零 |
3. 如图所示,质量为m,长为l的铜棒ab,用长度也为l的两根轻导线水平悬吊在竖直向上的匀强磁场中,磁感应强度为B,未通电时,轻导线静止在竖直方向,通入恒定电流后,棒向外偏转的最大角度为θ,则( )
如图所示,质量为m,长为l的铜棒ab,用长度也为l的两根轻导线水平悬吊在竖直向上的匀强磁场中,磁感应强度为B,未通电时,轻导线静止在竖直方向,通入恒定电流后,棒向外偏转的最大角度为θ,则( )
 如图所示,质量为m,长为l的铜棒ab,用长度也为l的两根轻导线水平悬吊在竖直向上的匀强磁场中,磁感应强度为B,未通电时,轻导线静止在竖直方向,通入恒定电流后,棒向外偏转的最大角度为θ,则( )
如图所示,质量为m,长为l的铜棒ab,用长度也为l的两根轻导线水平悬吊在竖直向上的匀强磁场中,磁感应强度为B,未通电时,轻导线静止在竖直方向,通入恒定电流后,棒向外偏转的最大角度为θ,则( )| A. | 棒中电流的方向为b→a | B. | 棒中电流的大小为$\frac{mgtanθ}{Bl}$ | ||
| C. | 棒中电流的大小为$\frac{mg(1-cosθ)}{Blsinθ}$ | D. | 若只增大轻导线的长度,则θ角变大 |
10. 如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )
如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )
 如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )
如图所示的实验装置中,小球A、B完全相同.用小锤轻击弹性金属片,A球沿水平方向抛出,同时B球被松开,自由下落,实验中两球同时落地.图中虚线1、2代表离地高度不同的两个水平面,则下列说法正确的是( )| A. | A球经过面1时的速率等于B球经过面1时的速率 | |
| B. | A球从面1到面2的速率变化等于B球从面1到面2的速率变化 | |
| C. | A球从面1到面2的动量变化大于B球从面1到面2的动量变化 | |
| D. | A球从面1到面2的机械能变化等于B球从面1到面2的机械能变化 |
8.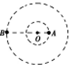 经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )
经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )
 经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )
经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由相距较近的恒星组成,每个恒星的半径远小于两个恒星之间的距离,而且双星系统一般远离其他天体,它们在相互间的万有引力作用下,绕某一点做匀速圆周运动,如图所示为某一双星系统,A星球的质量为m1,B星球的质量为m2,它们中心之间的距离为L,引力常量为G,则下列说法正确的是( )| A. | A星球的轨道半径为R=$\frac{{m}_{1}}{{m}_{1}+{m}_{2}}$L | |
| B. | B星球的轨道半径为r=$\frac{{m}_{2}}{{m}_{1}}$L | |
| C. | 双星运行的周期为T=2πL$\sqrt{\frac{L}{G({m}_{1}+{m}_{2})}}$ | |
| D. | 若近似认为B星球绕A星球中心做圆周运动,则B星球的运行周期为T=2πL$\sqrt{\frac{L}{G{m}_{1}}}$ |

 如图所示是游乐园内某种过山车的示意图.半径为R=5.0m的光滑圆形轨道固定在倾角为θ=37°的斜轨道面上的A点,圆轨道的最高点D与车(视为质点)的初始位置P点平齐,B为圆轨道的最低点,C点与圆心O等高,圆轨道与斜轨道PA之间平滑连接.小车从P点由静止开始下滑,恰好到达C点.已知g=10m/s2,sin37°=0.6,cos37°=0.8,车的质量m=100kg.求:
如图所示是游乐园内某种过山车的示意图.半径为R=5.0m的光滑圆形轨道固定在倾角为θ=37°的斜轨道面上的A点,圆轨道的最高点D与车(视为质点)的初始位置P点平齐,B为圆轨道的最低点,C点与圆心O等高,圆轨道与斜轨道PA之间平滑连接.小车从P点由静止开始下滑,恰好到达C点.已知g=10m/s2,sin37°=0.6,cos37°=0.8,车的质量m=100kg.求: 如图的电路中,电池组的电动势E=30伏,电阻R2=10欧,两个水平放置的带电金属板间的距离d=1.5厘米在金属板间的匀强电场中,有一质量为m=7×10-8千克带电量q=-7.0×10-10库仑的油滴,当把可变电阻器R3的阻值调到30欧姆接入电路时,带电油滴恰好静止悬浮在电场中,此时安培表示数I=1.5安培,试求:
如图的电路中,电池组的电动势E=30伏,电阻R2=10欧,两个水平放置的带电金属板间的距离d=1.5厘米在金属板间的匀强电场中,有一质量为m=7×10-8千克带电量q=-7.0×10-10库仑的油滴,当把可变电阻器R3的阻值调到30欧姆接入电路时,带电油滴恰好静止悬浮在电场中,此时安培表示数I=1.5安培,试求: