题目内容
1. 如图所示,两根平行金属导轨cd、ef置于水平面内,导轨之间接有电阻R,导轨处在竖直向下的匀强磁场中.金属棒ab静止在导轨上,abec为边长为L的正方形,金属棒电阻为r,其余电阻不计.t=0时匀强磁场的磁感应强度为B0,金属棒静止.若从t=0时刻起,磁感应强度均匀增加,每秒增加量为k,则( )
如图所示,两根平行金属导轨cd、ef置于水平面内,导轨之间接有电阻R,导轨处在竖直向下的匀强磁场中.金属棒ab静止在导轨上,abec为边长为L的正方形,金属棒电阻为r,其余电阻不计.t=0时匀强磁场的磁感应强度为B0,金属棒静止.若从t=0时刻起,磁感应强度均匀增加,每秒增加量为k,则( )| A. | 金属棒中的感应电流的方向为b→a | |
| B. | 金属棒中的感应电流的大小为$\frac{{k{L^2}}}{r}$ | |
| C. | 金属棒的电阻消耗的电功率为$\frac{{{k^2}{L^4}r}}{{{{(R+r)}^2}}}$ | |
| D. | 若t=t1时金属棒仍静止,则金属棒受到的静摩擦力大小为(B0+kt1)$\frac{{kL_{\;}^3}}{(R+r)}$ |
分析 磁感应强度B的变化率为k,根据法拉第电磁感应定律求解感应电动势大小,再由欧姆定律求出感应电流的大小,由楞次定律判断其方向.
磁感应强度B的表达式为B=B0+kt,由安培力公式F=BIL求出安培力,则由平衡条件得知,水平拉力与安培力大小相等.
解答 解:A、根据楞次定律知感应电流方向为逆时针,金属棒中的感应电流方向为:b→a,故A正确;
B、感应电动势:E=$\frac{△Φ}{△t}$=$\frac{△B}{△t}$S=kL2,金属棒中的感应电流:I=$\frac{E}{R+r}$=$\frac{k{L}^{2}}{R+r}$,故B错误;
C、金属棒消耗的电功率:P=I2r=$\frac{{k}^{2}{L}^{4}r}{(R+r)^{2}}$,故C正确;
D、t=t1时采用电动势:B=B0+kt1,金属棒受到的安培力:F=BIL=$\frac{k({B}_{0}+k{t}_{1}){L}^{3}}{R+r}$,
金属棒静止,由平衡条件得,摩擦力:f=$\frac{k({B}_{0}+k{t}_{1}){L}^{3}}{R+r}$,故D正确;
故选:ACD.
点评 本题根据法拉第电磁感应定律求解感应电动势,由欧姆定律和安培力公式推导安培力的表达式,是常用的方法和思路;本题考查了法拉第电磁感应定律、楞次定律、安培力公式的基本运用,注意磁感应强度均匀变化,面积不变,则感应电动势不变,但是导体棒所受的安培力在变化.

练习册系列答案
相关题目
11.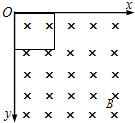 如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )
如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )
 如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )
如图所示,一边长为L,质量为m,电阻为R的正方形金属框竖直放置在磁场中,磁场方向垂直方框平面向里,磁感应强度B的大小随y的变化规律为B=B0+ky(k为常数且大于零),同一水平面上的磁感应强度相同.现将方框从图示位置水平向右抛出,已知重力加速度为g,磁场区域足够大,不计空气阻力,则( )| A. | 线框将一直做曲线运动 | |
| B. | 线框最终将做直线运动 | |
| C. | 线框最终的速度大于$\frac{mgR}{{k}^{2}{L}^{4}}$ | |
| D. | 线框中产生的感应电流沿顺时针方向 |
12.对于经典力学理论,下列说法正确的是( )
| A. | 由于相对论、量子论的提出,经典力学已经失去了它的意义 | |
| B. | 经典力学在今天广泛应用,它的正确性无可怀疑,仍是普遍适用的 | |
| C. | 经典力学在历史上起了巨大的作用,随着物理学的发展而逐渐过时,成为一种古老的理论 | |
| D. | 经典力学在宏观低速运动中,引力不太大时适用 |
9. 如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
 如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )
如图所示,用r表示两个分子间的距离,用Ep表示两个分子之间的势能,当r=r0时两分子间斥力等于引力,设两个分子相距很远时Ep=0,则( )| A. | 当r<r0时,Ep随r的增大而增大 | B. | 当r>r0时,Ep随r的增大而增大 | ||
| C. | 当r<r0时,Ep不随r的变化而变化 | D. | 当r=r0时,Ep=0 |
6. 两个固定的等量异种电荷,在他们连线的垂直平分线上有a、b、c、d四点,相邻两点间距离相等,如图所示,下列说法正确的是( )
两个固定的等量异种电荷,在他们连线的垂直平分线上有a、b、c、d四点,相邻两点间距离相等,如图所示,下列说法正确的是( )
 两个固定的等量异种电荷,在他们连线的垂直平分线上有a、b、c、d四点,相邻两点间距离相等,如图所示,下列说法正确的是( )
两个固定的等量异种电荷,在他们连线的垂直平分线上有a、b、c、d四点,相邻两点间距离相等,如图所示,下列说法正确的是( )| A. | a点电势比b点电势高 | |
| B. | a、b两点场强方向相同,a点场强比b点大 | |
| C. | b、d两点场强相等 | |
| D. | 一带电粒子(不计重力),在a点无初速释放,则它将在a、b 线上运动 |
3. 如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点,测得四个时刻物体的瞬时速度记录在下表中,取g=10m/s2.求:
如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点,测得四个时刻物体的瞬时速度记录在下表中,取g=10m/s2.求:
(1)物体经过B点时的速度;
(2)物体从开始运动到C点所需时间;
(3)A、B间的距离和B、C间的距离.
 如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点,测得四个时刻物体的瞬时速度记录在下表中,取g=10m/s2.求:
如图所示,t=0时,质量为0.5kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点,测得四个时刻物体的瞬时速度记录在下表中,取g=10m/s2.求:(1)物体经过B点时的速度;
(2)物体从开始运动到C点所需时间;
(3)A、B间的距离和B、C间的距离.
| t/s | 0 | 1 | 2 | 4 | 6 |
| v/(m•s-1) | 0 | 4 | 8 | 12 | 8 |
4. 一束红光和一束紫光以相同的角度沿半径方向射向截面为半圆形的玻璃砖,并分别沿OA和OB方向射出,如图所示,下列说法正确的是( )
一束红光和一束紫光以相同的角度沿半径方向射向截面为半圆形的玻璃砖,并分别沿OA和OB方向射出,如图所示,下列说法正确的是( )
 一束红光和一束紫光以相同的角度沿半径方向射向截面为半圆形的玻璃砖,并分别沿OA和OB方向射出,如图所示,下列说法正确的是( )
一束红光和一束紫光以相同的角度沿半径方向射向截面为半圆形的玻璃砖,并分别沿OA和OB方向射出,如图所示,下列说法正确的是( )| A. | OA是红光 | |
| B. | OB是红光 | |
| C. | OA穿过玻璃砖的时间较短 | |
| D. | OA的频率比OB的频率小 | |
| E. | 在真空中,OA的传播速度比OB的传播速度大 |