题目内容
14. 如图所示,一物块从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.测得每隔3s的三个时刻物体的瞬时速度,记录在下表中.g取10m/s2,
如图所示,一物块从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.测得每隔3s的三个时刻物体的瞬时速度,记录在下表中.g取10m/s2,| t/s | 0 | 3 | 6 | 9 |
| v(m/s) | 0 | 8 | 12 | 8 |
(2)求B点速度;
(3)求AB段和BC段的距离.
分析 根据图表中的数据,由运动学公式可以求出物体下滑的加速度和在水平面上的加速度.如果第6s还在斜面上的话,求出第6s末的速度,从而判断出第6s已过B点.通过运动学公式求出vB,即可求出AB、BC的距离.
解答 解:(1、2)根据图表中的数据,可以求出物体下滑的加速度 a1=$\frac{△v}{△t}$=$\frac{8}{3}$m/s2,若t=6s时刻物体恰好经过B点时,B点的速度为 vB=a1t=$\frac{8}{3}×6m/s$=16m/s>12m/s.所以第6s已过B点,同样根据图表数据可知,物体在水平面上滑动时的加速度${a}_{2}=\frac{△v}{△t}=\frac{8-12}{9-6}m/{s}^{2}=-\frac{4}{3}m/{s}^{2}$,则设物体在斜面上滑行时间为t1,从斜面底端到速度为12m/s的时间为t2. 则有:
a1t1+a2t2=12m/s
t1+t2=6s
解得t1=5s,即物体加速5s后到达B点,此时${v}_{B}={a}_{1}{t}_{1}=\frac{8}{3}×5m/s=\frac{40}{3}m/s$
从B开始减速至物体停止,由速度时间关系可得在BC段运动的时间${t}_{3}=\frac{0-{v}_{B}}{{a}_{2}}=\frac{0-\frac{40}{3}}{-\frac{4}{3}}s=10s$
(3)物体在AB段做初速度为零的匀加速运动,可得${x}_{AB}=\frac{1}{2}{a}_{1}{t}_{1}^{2}=\frac{1}{2}×\frac{8}{3}×{5}^{2}m$=$\frac{100}{3}m$,物体在BC段运动的位移${x}_{BC}={v}_{B}{t}_{3}+\frac{1}{2}{a}_{2}{t}_{3}^{2}$=$\frac{40}{3}×10+\frac{1}{2}×(-\frac{4}{3})×1{0}^{2}m$=$\frac{200}{3}m$
答:(1)AB段所用时间为5s,BC段所用时间为10s;
(2)到达B点时的速度为$\frac{40}{3}m/s$;
(3)AB段的距离为$\frac{100}{3}m$,BC段的距离为$\frac{200}{3}m$.
点评 解决本题的关键熟练掌握运动学公式v2-v02=2ax、v=v0+at,并能通过计算分析物体的运动过程,不能凭感觉认为6s末物体的速度最大刚好到达B点.

 质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 克服摩擦力做功$\frac{1}{4}$mgh | ||
| C. | 动能损失了mgh | D. | 机械能损失了$\frac{1}{2}$mgh |
| A. | 2 N | B. | 10 N | C. | 14 N | D. | 48 N |
| A. | 异名磁极相互吸引,同名磁极相互排斥,都是通过磁场发生的相互作用 | |
| B. | 磁感线可以形象地描述各点的磁场的强弱和方向,磁感线上每一点的切线方向都和小磁针在该点静止时S极所指的方向一致 | |
| C. | 穿过线圈的磁通量为零时,磁感应强度不一定为零 | |
| D. | 磁感应强度越大,穿过闭合回路的磁通量也越大 |
 如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )
如图所示,与水平地面夹角为锐角的下面低端A向上有三个等间距点B、C和D,即AB=BC=CD.小滑块P以初速v从A出发,沿斜面向上运动.先设置斜面与滑块间处处无摩擦,则滑块到达D位置刚好停下,而后下滑.若设置斜面 AB部分与滑块间有处处相同的摩擦,其余部位与滑块间仍无摩擦,则滑块上行到C位置刚好停下,而后下滑.滑块下滑到B位置时速度以及回到 A端时速度大小分别为( )| A. | $\frac{v}{2}$、$\frac{\sqrt{3}v}{3}$ | B. | $\frac{\sqrt{3}v}{3}$、$\frac{\sqrt{3}v}{3}$ | C. | $\frac{v}{2}$、$\frac{\sqrt{3}v}{2}$ | D. | $\frac{v}{2}$、$\frac{v}{2}$ |



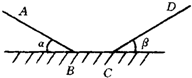 如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求:
如图所示,一个滑块质量为2kg,从斜面上A点由静止下滑,经过BC平面又冲上另一斜面到达最高点D.已知AB=100cm,CD=60cm,∠α=30°,∠β=37°,且AB、CD均光滑,只有BC面粗糙,BC=28cm且BC面上各处粗糙程度相同,(g取10m/s2)试求: