题目内容
14.“神舟”六号飞船一飞冲天,一举成功,再次把中国人“巡天遥看一天河”的陆地梦想变成“手可摘星辰,揽明月”的太空现实.“神舟”六号飞船点火发射时,飞船处于一个加速过程,在加速过程中宇航员处于超重状态.人们把这种状态下宇航员所受支持力FN与在地表面时重力mg的比值K=$\frac{{F}_{N}}{mg}$称为载荷值.(1)假设宇航员在超重状态下载荷值的最大值为K=7,飞船带着宇航员竖直向上发射时的加速度a的最大值为多少?(已知地球表面的重力加速度g=10m/s2.)
(2)“神舟”六号飞船发射成功后,进入圆形轨道稳定运行,运转一圈的时间为T,地球的半径为R,表面的重力加速度为g,万有引力常量为G,试求这一圆形轨道距离地面的高度H.(用R、g、T、G表示)
分析 (1)运用牛顿第二定律对宇航员研究F-mg=ma,因为F=kmg,所以kmg-mg=ma,a越大,k越大,为了保护宇航员的安全,k最大只能取7,把7代入,即得a的最大值.
(2)飞船绕地球做圆周运动所需向心力由地球对飞船的万有引力提供,由牛顿第二定律可以分析答题.
解答 解:(1)由牛顿第二定律可知:${F}_{N}^{\;}-mg=ma$,
由题意可知:$k=\frac{{F}_{N}^{\;}}{mg}$,整理得:mg(k-1)=ma,
将k=7代入解得:$a=60m/{s}_{\;}^{2}$;
(2)设地球的质量为 M,飞船的质量为m,飞船距地面高为h,万有引力充当向心力,由牛顿第二定律得:
$G\frac{Mm}{(R+h)_{\;}^{2}}=m(\frac{2π}{T})_{\;}^{2}(R+h)$,
在地球表面附近,重力等于万有引力,即:$G\frac{Mm}{{R}_{\;}^{2}}=mg$,
解得:$h=\root{3}{\frac{g{T}_{\;}^{2}{R}_{\;}^{2}}{4{π}_{\;}^{2}}}-R$;
答:(1)假设宇航员在超重状态下载荷值的最大值为K=7,飞船带着宇航员竖直向上发射时的加速度a的最大值为$60m/{s}_{\;}^{2}$
(2)“神舟”六号飞船发射成功后,进入圆形轨道稳定运行,运转一圈的时间为T,地球的半径为R,表面的重力加速度为g,万有引力常量为G,这一圆形轨道距离地面的高度H为$\root{3}{\frac{g{T}_{\;}^{2}{R}_{\;}^{2}}{4{π}_{\;}^{2}}}-R$
点评 飞船绕地球最圆周运动,万有引力提供向心力,应用万有引力定律、牛顿第二定律即可正确解题

练习册系列答案
相关题目
4. 如图所示,质量为m的小球固定在长为L的轻直杆的一端,并以轻杆的另一端为圆心在竖直面内做圆周运动.在小球转速逐渐增大的过程中,小球的最高点时( )
如图所示,质量为m的小球固定在长为L的轻直杆的一端,并以轻杆的另一端为圆心在竖直面内做圆周运动.在小球转速逐渐增大的过程中,小球的最高点时( )
 如图所示,质量为m的小球固定在长为L的轻直杆的一端,并以轻杆的另一端为圆心在竖直面内做圆周运动.在小球转速逐渐增大的过程中,小球的最高点时( )
如图所示,质量为m的小球固定在长为L的轻直杆的一端,并以轻杆的另一端为圆心在竖直面内做圆周运动.在小球转速逐渐增大的过程中,小球的最高点时( )| A. | 小球的最小速度是$\sqrt{Lg}$ | |
| B. | 轻杆对小球的作用力逐渐增大 | |
| C. | 轻杆对小球的作用力逐渐减小 | |
| D. | 轻杆对小球的作用力可能先减小后增大 |
5. 如图所示,在一个带活塞的容器底部有一定量的水,现保持温度不变,上提活塞,平衡后底部仍有部分水,则( )
如图所示,在一个带活塞的容器底部有一定量的水,现保持温度不变,上提活塞,平衡后底部仍有部分水,则( )
 如图所示,在一个带活塞的容器底部有一定量的水,现保持温度不变,上提活塞,平衡后底部仍有部分水,则( )
如图所示,在一个带活塞的容器底部有一定量的水,现保持温度不变,上提活塞,平衡后底部仍有部分水,则( )| A. | 液面上方水蒸气的密度和压强都不变 | |
| B. | 液面上方水蒸气的质量增加,密度减小 | |
| C. | 液面上方水蒸气的密度减小,压强减小 | |
| D. | 液面上方的水蒸气从饱和变成未饱和 |
9.关于运动的合成与分解,下列说法中正确的是( )
| A. | 两个速度大小不等的匀速直线运动的合运动一定是匀速直线运动 | |
| B. | 两个直线运动的合运动一定是直线运动 | |
| C. | 合速度大小可以小于分速度大小 | |
| D. | 由两个分速度的大小就可以确定合运动速度的大小 |
19. 如图所示,电路与一绝热密闭气缸相连,R为电热丝,气缸内有一定质量的理想气体,外界大气压恒定.闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法中正确的是( )
如图所示,电路与一绝热密闭气缸相连,R为电热丝,气缸内有一定质量的理想气体,外界大气压恒定.闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法中正确的是( )
 如图所示,电路与一绝热密闭气缸相连,R为电热丝,气缸内有一定质量的理想气体,外界大气压恒定.闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法中正确的是( )
如图所示,电路与一绝热密闭气缸相连,R为电热丝,气缸内有一定质量的理想气体,外界大气压恒定.闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法中正确的是( )| A. | 气体的内能增加 | |
| B. | 气体分子平均动能不变 | |
| C. | 电热丝放出的热量等于气体对外所做的功 | |
| D. | 气体的压强不变 |
3.当分子间距离大于10r0(r0是分子平衡位置间距离)时,分子力可以认为是零,规定此时分子势能为零,当分子间距离是平衡距离r0时,下面的说法中正确的是( )
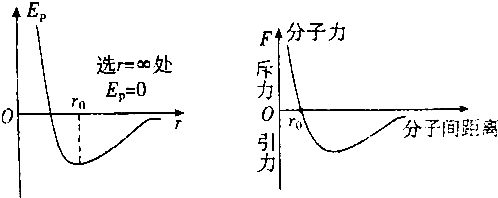

| A. | 分子力是零,分子势能也是零 | B. | 分子力是零,分子势能不是零 | ||
| C. | 分子力不是零,分子势能是零 | D. | 分子力不是零,分子势能不是零 |
4.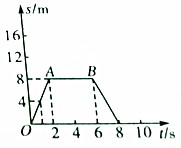 如图所示是质点在0~8s内的位移-时间图象,下列说法正确的是( )
如图所示是质点在0~8s内的位移-时间图象,下列说法正确的是( )
 如图所示是质点在0~8s内的位移-时间图象,下列说法正确的是( )
如图所示是质点在0~8s内的位移-时间图象,下列说法正确的是( )| A. | 质点在第1s的位移为4m | |
| B. | 质点在第1s末的速度为4m/s | |
| C. | 点在2s~4s内做匀速直线运动 | |
| D. | 质点在前2s和最后2s的运动方向相反,但前2s速度更大 |