题目内容
18. 如图所示,一带电量为+q、质量为m的粒子从O点以一定的初速射入宽度为2R的匀强电场,电场方向竖直向上,经一段时间后,从A点沿水平方向离开电场,并进入圆形匀强磁场区域,磁场区域左端与电场区域的右边界相切,磁场区域半径为R,磁感应强度为B,方向垂直于纸面向内.水平速度方向与如图直径平行且相距0.6R,若带电粒子在磁场中偏转90°后离开磁场(粒子重力不计).求:
如图所示,一带电量为+q、质量为m的粒子从O点以一定的初速射入宽度为2R的匀强电场,电场方向竖直向上,经一段时间后,从A点沿水平方向离开电场,并进入圆形匀强磁场区域,磁场区域左端与电场区域的右边界相切,磁场区域半径为R,磁感应强度为B,方向垂直于纸面向内.水平速度方向与如图直径平行且相距0.6R,若带电粒子在磁场中偏转90°后离开磁场(粒子重力不计).求:(1)粒子在磁场中运动的速度;
(2)粒子从进入电场到离开磁场的总时间.
分析 (1)作出粒子在磁场中的运动轨迹,求出粒子的轨道半径,然后由牛顿第二定律求出粒子在磁场中运动的速度.
(2)求出粒子在电场中的运动时间,求出粒子在磁场中的运动时间,然后求出粒子从进入电场到离开磁场的总时间.
解答 解:(1)粒子在磁场中的运动轨迹如图所示:
粒子在磁场中偏转90°后离开磁场,
由几何知识可知,θ=45°,α=45°-β,
水平速度方向与如图直径平行且相距0.6R,
则:sinβ=$\frac{0.6R}{R}$=0.6,
由几何知识(正弦定理)得:
$\frac{R}{sinθ}$=$\frac{r}{sinα}$,即:$\frac{R}{sin45°}$=$\frac{r}{sin(45°-β)}$,
解得:r=0.2R,
粒子在磁场中做圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,解得:v=$\frac{qBR}{5m}$;
(2)粒子受到的电场力竖直向上,在水平方向不受力,
粒子在电场中沿水平方向做匀速直线运动,
由题意可知,粒子从A点沿水平方向离开电场进入磁场,
则粒子在水平方向的速度等于粒子在磁场中做匀速圆周运动的速度:v=$\frac{qBR}{5m}$,
粒子在电场中的运动时间:t1=$\frac{2R}{v}$=$\frac{2R}{\frac{qBR}{5m}}$=$\frac{10m}{qB}$,
粒子在磁场中做匀速圆周运动的周期:T=$\frac{2πm}{qB}$,
粒子在磁场中的运动时间:t2=$\frac{2θ}{360°}$T=$\frac{90°}{360°}$×$\frac{2πm}{qB}$=$\frac{πm}{2qB}$,
粒子从进入电场到离开磁场的总时间:t=t1+t0+t2=$\frac{(20+π)m}{2qB}$+$\frac{0.2R}{\frac{qBR}{5m}}$=$\frac{22+π}{2qB}m$;
答:(1)粒子在磁场中运动的速度为$\frac{qBR}{5m}$;
(2)粒子从进入电场到离开磁场的总时间$\frac{22+π}{2qB}m$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程是正确解题的关键,处理粒子在磁场中的运动,要根据题意作出粒子运动轨迹,确定粒子做圆周运动的圆心位置,应用几何知识求出粒子轨道半径,这是解题的一半思路,也是解题的关键.

 阅读快车系列答案
阅读快车系列答案
| A. | 该波的波速为100m/s | |
| B. | 图乙时刻Q点的振动方向沿y正方向 | |
| C. | 波源开始振动方向沿y负方向 | |
| D. | 从t=0开始,经0.05s,Q的路程为10cm |
 上下做简谐振动的振源O在t=0时开始向上振动,振幅A=10cm,形成的波沿匀质弹性绳向右传播,t=0.4s时第一次形成如图所示的波形,则( )
上下做简谐振动的振源O在t=0时开始向上振动,振幅A=10cm,形成的波沿匀质弹性绳向右传播,t=0.4s时第一次形成如图所示的波形,则( )| A. | 振源的振动周期为0.4s | |
| B. | 该波的波速为20m/s | |
| C. | 从t=0到t=0.4s内,x=4m处的质点B运动的路程为40cm | |
| D. | 从t=0.4s时刻开始,质点A比质点C先回到平衡位置 |
 水平面上有一边长为L的正方形,其a、b、c三个顶点上分别放置了三个等量的正点电荷Q,将一个电量为+q的点电荷A分别放在正方形中心点O点和正方形的另一个顶点d点处,以下正确的叙述有( )
水平面上有一边长为L的正方形,其a、b、c三个顶点上分别放置了三个等量的正点电荷Q,将一个电量为+q的点电荷A分别放在正方形中心点O点和正方形的另一个顶点d点处,以下正确的叙述有( )| A. | A在d点所受的电场力大于其在O点所受的电场力 | |
| B. | A在d点所具有的电势能大于其在O点所具有的电势能 | |
| C. | A在d点的加速度方向,与在O点的加速度方向相同 | |
| D. | A在d点和O点的电势能数值都是大于零的 |
 如图所示,运动员的双手握紧竖直放置的圆形器械,若手臂OA、OB的拉力分别是FA、FB,手臂OB不动,在手臂OA由水平方向缓慢移到OA′位置过程中,下列表述正确的是( )
如图所示,运动员的双手握紧竖直放置的圆形器械,若手臂OA、OB的拉力分别是FA、FB,手臂OB不动,在手臂OA由水平方向缓慢移到OA′位置过程中,下列表述正确的是( )| A. | FA变大 | B. | FA与FB的合力始终不变 | ||
| C. | FA的大小保持不变 | D. | FB变小 |
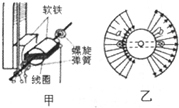 如图甲是磁电式电流表的结构.如图乙所示,蹄型磁铁和铁芯间的磁场均匀辐向分布,边长为l的正方形线圈中通以电流I,线圈的a导线电流方向垂直纸面向外,b导线电流方向垂直纸面向内,a、b两条导线所在处的磁感应强度大小为B,则( )
如图甲是磁电式电流表的结构.如图乙所示,蹄型磁铁和铁芯间的磁场均匀辐向分布,边长为l的正方形线圈中通以电流I,线圈的a导线电流方向垂直纸面向外,b导线电流方向垂直纸面向内,a、b两条导线所在处的磁感应强度大小为B,则( )| A. | 该磁场是匀强磁场 | B. | 该线圈的磁通量为Bl2 | ||
| C. | a导线受到的安培力方向向下 | D. | b导线受到安培力大小为IlB |

 如图所示,ab为平行金属板,其板面与纸面垂直,用导线与光滑的(电阻不计)足够长的平行金属轨道cd连接,轨道cd都垂直于匀强磁场,且与ab在同一平面内,阻值为R的电阻与cd相连,若磁感应强度为B,方向如图所示,a与b、c与d均相距为L,现有一根电阻为0.5R的金属棒MN紧贴在cd轨道上,在外力作用下,MN棒始终垂直于cd匀速滑动,要使一质量不计的带电粒子,在ab间以速度V0水平向右作匀速直线运动,求:
如图所示,ab为平行金属板,其板面与纸面垂直,用导线与光滑的(电阻不计)足够长的平行金属轨道cd连接,轨道cd都垂直于匀强磁场,且与ab在同一平面内,阻值为R的电阻与cd相连,若磁感应强度为B,方向如图所示,a与b、c与d均相距为L,现有一根电阻为0.5R的金属棒MN紧贴在cd轨道上,在外力作用下,MN棒始终垂直于cd匀速滑动,要使一质量不计的带电粒子,在ab间以速度V0水平向右作匀速直线运动,求: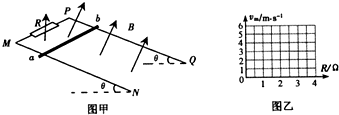 如图甲,MN、PQ是两条间距为L=2m的光滑平行金属轨道,轨道平面与水平面的夹角为θ=30.(轨道足够长且电阻不计).M、P之间连接一电阻箱R,导轨处于磁场方向垂直于轨道平面向上,磁感应强度大小为B=0.5T的匀强磁场中.一条质量为m=0.2kg的金属杆a b水平置于轨道上,其接入电路的电阻值为r=1.0Ω.现静止释放杆a b (杆下滑过程中跟轨道接触良好且始终与轨道垂直),g取10m/s2.试求:
如图甲,MN、PQ是两条间距为L=2m的光滑平行金属轨道,轨道平面与水平面的夹角为θ=30.(轨道足够长且电阻不计).M、P之间连接一电阻箱R,导轨处于磁场方向垂直于轨道平面向上,磁感应强度大小为B=0.5T的匀强磁场中.一条质量为m=0.2kg的金属杆a b水平置于轨道上,其接入电路的电阻值为r=1.0Ω.现静止释放杆a b (杆下滑过程中跟轨道接触良好且始终与轨道垂直),g取10m/s2.试求: