题目内容
14.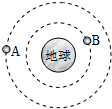 如图所示,人造卫星A、B在同一平面内绕地球做匀速圆周运动.则卫星A的线速度小于卫星B的线速度,卫星A的加速度小于卫星B的加速度(选填“大于”、“小于”或“等于”).
如图所示,人造卫星A、B在同一平面内绕地球做匀速圆周运动.则卫星A的线速度小于卫星B的线速度,卫星A的加速度小于卫星B的加速度(选填“大于”、“小于”或“等于”).
分析 根据万有引力提供向心力得出线速度、向心加速度与轨道半径的关系,从而比较出大小.
解答 解:根据万有引力提供向心力得$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=ma$,解得:a=$\frac{GM}{{r}^{2}}$,v=$\sqrt{\frac{GM}{r}}$,则轨道半径越大,线速度越小、加速度越小,所以卫星A的线速度小于卫星B的线速度,卫星A的加速度小于卫星B的加速度.
故答案为:小于;小于.
点评 解决本题的关键掌握万有引力提供向心力这一理论,知道线速度、角速度、加速度、周期与轨道半径的关系.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
4. 如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )
如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )
 如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )
如图所示的装置中,A、B、C的半径分别为r、2r、4r,B、C为一轮轴上的大小两个轮,皮带在传动AB轮的过程中不打滑,b点到圆心的距离为r,a、c、d分别是A、B、C三个轮子边缘上的三个点,则图中a、b、c、d各点的线速度之比、角速度之比、角速度之比正确的是( )| A. | va:vb:vc:vd=2:1:2:6 | B. | ωa:ωb:ωc:ωd=2:1:1:1 | ||
| C. | aa:ab:ac:ad=4:1:2:4 | D. | aa:ab:ac:ad=4:1:2:6 |
5.一半径为R、质量可视为均匀分布的球形行星的密度为ρ,自转周期为T0,若万有引力常量为G,则( )
| A. | 该行星表面重力加速度在两极的大小为$\frac{4}{3}$GρRπ | |
| B. | 该行星的卫星在星球表面附近做圆周运动的速率为2πR$\sqrt{\frac{3π}{ρG}}$ | |
| C. | 该行星的同步卫星的轨道半径为R($\frac{ρG{T}_{0}^{2}}{3π}$)${\;}^{\frac{1}{3}}$ | |
| D. | 该行星的同步卫星的运行速率为$\frac{2πR}{{T}_{0}}$ |
2. 如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )
如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )
 如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )
如图所示,半圆形玻璃砖按图中实线位置放置,直径与BD重合.一束激光沿着半圆形玻璃砖的半径从圆弧面垂直BD射到圆心O点上.使玻璃砖绕O点逆时针缓慢地转过角度θ(0°<θ<90°),观察到折射光斑和反射光斑在弧形屏上移动.在玻璃砖转动过程中,以下说法正确的是( )| A. | 折射光斑在弧形屏上沿C→F→B方向移动 | |
| B. | 折射光斑的亮度逐渐变暗 | |
| C. | 折射角一定大于反射角 | |
| D. | 反射光线转过的角度为θ | |
| E. | 当玻璃砖转至θ=45°时,恰好看不到折射光线.则此玻璃砖的折射率n=$\sqrt{2}$ |
19. 在两固定的竖直挡板间有一表面光滑的重球,球的直径略小于挡板间的距离,用一横截面为直角三角形的楔子抵住.楔子的底角为60°,重力不计.设最大静摩擦力等于滑动摩擦力.为使球不下滑,楔子与挡板间的动摩擦因数至少应为( )
在两固定的竖直挡板间有一表面光滑的重球,球的直径略小于挡板间的距离,用一横截面为直角三角形的楔子抵住.楔子的底角为60°,重力不计.设最大静摩擦力等于滑动摩擦力.为使球不下滑,楔子与挡板间的动摩擦因数至少应为( )
 在两固定的竖直挡板间有一表面光滑的重球,球的直径略小于挡板间的距离,用一横截面为直角三角形的楔子抵住.楔子的底角为60°,重力不计.设最大静摩擦力等于滑动摩擦力.为使球不下滑,楔子与挡板间的动摩擦因数至少应为( )
在两固定的竖直挡板间有一表面光滑的重球,球的直径略小于挡板间的距离,用一横截面为直角三角形的楔子抵住.楔子的底角为60°,重力不计.设最大静摩擦力等于滑动摩擦力.为使球不下滑,楔子与挡板间的动摩擦因数至少应为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图所示,足够长的直线ab靠近通电螺线管的一端,且与螺线管垂直.用磁传感器测量ab上各点沿ab方向上的磁感应强度分量Bx的大小,在计算机屏幕上显示的图象大致是( )
如图所示,足够长的直线ab靠近通电螺线管的一端,且与螺线管垂直.用磁传感器测量ab上各点沿ab方向上的磁感应强度分量Bx的大小,在计算机屏幕上显示的图象大致是( )







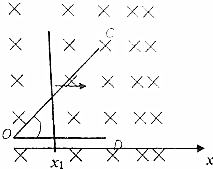 如图.水平面内有一“∠”型光滑金属导轨COD,电阻不计,∠COD=45°.足够长直导体棒搁在导轨上,单位长度的电阻为r=0.5Ω,导体棒垂直OD.空间存在垂直于导轨平面的磁场,以O点为原点沿0D方向建立坐标轴,导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,变化率为0.5T/m,O点磁感应强度B0=1T.在外力作用下,棒以一定的初速度向右做直线运动,运动时回路中的电流强度保持不变.已知运动到图中x1=1m位置时,速度大小v1=2m/s,则回路中的电流强度大小为6A,从x1=1m位置再向右运动1m的过程中,通过导体棒的电量为3.5C.
如图.水平面内有一“∠”型光滑金属导轨COD,电阻不计,∠COD=45°.足够长直导体棒搁在导轨上,单位长度的电阻为r=0.5Ω,导体棒垂直OD.空间存在垂直于导轨平面的磁场,以O点为原点沿0D方向建立坐标轴,导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,变化率为0.5T/m,O点磁感应强度B0=1T.在外力作用下,棒以一定的初速度向右做直线运动,运动时回路中的电流强度保持不变.已知运动到图中x1=1m位置时,速度大小v1=2m/s,则回路中的电流强度大小为6A,从x1=1m位置再向右运动1m的过程中,通过导体棒的电量为3.5C.