题目内容
6.若有一颗行星,其质量是地球的q倍,半径是地球的p倍,则该行星近地卫星的角速度是地球近地卫星的角速度的( )| A. | $\sqrt{pq}$ | B. | $\sqrt{\frac{q}{{p}^{3}}}$ | C. | $\sqrt{q{p}^{3}}$ | D. | $\sqrt{\frac{p}{q}}$ |
分析 根据万有引力提供向心力求出近地卫星的角速度的表达式,结合行星和地球的质量之比和半径之比,求出近地卫星的角速度之比.
解答 解:根据$G\frac{Mm}{{R}^{2}}=mR{ω}^{2}$得,ω=$\sqrt{\frac{GM}{{R}^{3}}}$,
因为行星的质量是地球质量的q倍,半径是地球的p倍,则行星近地卫星的角速度是地球近地卫星角速度的$\sqrt{\frac{q}{{p}^{3}}}$倍,故B正确,A、C、D错误.
故选:B.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,知道角速度与轨道半径和中心天体质量的关系,基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
12.行星冲日指的是当地球恰好运行到某地外行星和太阳之间,且三者几乎排成一条直线的现象.2014年4月9日发生了火星冲日现象.已知火星和地球绕太阳公转的方向相同,其轨迹近似为圆,火星的公转半径为地球的1.5倍,以下说法正确的是( )
| A. | 火星公转周期比地球小 | B. | 火星运行速度比地球大 | ||
| C. | 每年都会出现火星冲日现象 | D. | 2015年一定没有出现火星冲日现象 |
13.一根弹簧下端挂50g的钩码时,弹簧长8cm;挂100g的钩码时,弹簧长10cm.弹簧原长是( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
14.甲、乙两物体都做匀速圆周运动,其转动半径之比为3:2,在相等时间里甲转过75°,乙转过45°,则它们向心加速度之比为( )
| A. | 5:2 | B. | 5:4 | C. | 25:6 | D. | 25:12 |
11.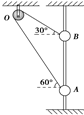 如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )
如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )
 如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )
如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则杆对A、B的弹力之比为( )| A. | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{1}$ | B. | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{3}$ | C. | $\frac{{N}_{A}}{{N}_{B}}=\frac{\sqrt{3}}{2}$ | D. | $\frac{{N}_{A}}{{N}_{B}}=\frac{2}{\sqrt{3}}$ |
15. 近年来我国高速铁路发展迅速,现已知某新型国产机车总质量为m,如图已知两轨间宽度为L,内外轨高度差为h,重力加速度为g,如果机车要进入半径为R的弯道,请问,该弯道处的设计速度最为适宜的是( )
近年来我国高速铁路发展迅速,现已知某新型国产机车总质量为m,如图已知两轨间宽度为L,内外轨高度差为h,重力加速度为g,如果机车要进入半径为R的弯道,请问,该弯道处的设计速度最为适宜的是( )
 近年来我国高速铁路发展迅速,现已知某新型国产机车总质量为m,如图已知两轨间宽度为L,内外轨高度差为h,重力加速度为g,如果机车要进入半径为R的弯道,请问,该弯道处的设计速度最为适宜的是( )
近年来我国高速铁路发展迅速,现已知某新型国产机车总质量为m,如图已知两轨间宽度为L,内外轨高度差为h,重力加速度为g,如果机车要进入半径为R的弯道,请问,该弯道处的设计速度最为适宜的是( )| A. | $\sqrt{\frac{gRh}{\sqrt{{L}^{2}-{h}^{2}}}}$ | B. | $\sqrt{\frac{gRh}{\sqrt{{L}^{2}-{R}^{2}}}}$ | C. | $\sqrt{\frac{gR\sqrt{{L}^{2}-{h}^{2}}}{h}}$ | D. | $\sqrt{\frac{gRL}{h}}$ |
16. 在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度方向可能是( )
在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度方向可能是( )
 在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度方向可能是( )
在xOy平面中有一通电直导线与Ox、Oy轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与Oz轴的正方向相同.该磁场的磁感应强度方向可能是( )| A. | 沿x轴负方向 | B. | 沿y轴负方向 | C. | 沿z轴正方向 | D. | 沿z轴负方向 |
