题目内容
11. 如图,半径为R的光滑圆轨道固定在竖直面内,一质量为m的小球沿轨道做完整的圆周运动,已知当地重力加速度大小为g,小球在最高点时对轨道的压力大小为mg,则小球在最低点时对轨道的压力大小为( )
如图,半径为R的光滑圆轨道固定在竖直面内,一质量为m的小球沿轨道做完整的圆周运动,已知当地重力加速度大小为g,小球在最高点时对轨道的压力大小为mg,则小球在最低点时对轨道的压力大小为( )| A. | 4mg | B. | 5mg | C. | 6mg | D. | 7mg |
分析 对最高点分析,根据向心力公式可求得最高点的速度,再对由最高点到最低点过程根据机械能守恒定律可求得最低点的速度,再对最低点根据向心力公式可求得小球受到的支持力,再根据牛顿第三定律可求得对轨道的压力.
解答 解:根据向心力公式可知,在最高点时:
mg+F=m$\frac{{v}^{2}}{r}$
根据机械能守恒定律可知,
mg2r=$\frac{1}{2}$mv12-$\frac{1}{2}$mv2
再对最低点分析可知:
F′-mg=m$\frac{{v}_{1}^{2}}{r}$
联立解得:F’=7mg;
则由牛顿第三定律可知,小球对轨道的压力为7mg.
故选:D.
点评 本题考查向心力公式的应用以及机械能守恒定律的应用,要注意正确分析物理过程,明确最高点和最低点的受力分析,明确向心力的来源是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.质量为m的物体自由下落,不计空气阻力,在ts内,重力对物体做功的平均功率是( )
| A. | $\frac{m{g}^{2}t}{2}$ | B. | mg2t | C. | 0 | D. | $\frac{m{g}^{2}t}{4}$ |
2.如图所示,O点是竖直圆环的顶点,Oc是圆环直径,Oa和Ob是两条不同倾角的弦.在Oc、Oa、Ob线上置三个光滑的斜面,一个质点从O自由释放,先后分别沿Oc、Oa、Ob下滑,到达a、b、c三点的时间( )


| A. | 最短的是a点 | B. | 最短的是b点 | C. | 最长的是c点 | D. | 时间都相同 |
19.有两个简谐运动x1=3asin(4πbt+$\frac{π}{4}$),x2=9asin(8πbt+$\frac{π}{4}$),则他的振幅、周期之比正确的是( )
| A. | A1:A2=1:3,T1:T2=1:2 | B. | A1:A2=1:3,T1:T2=2:1 | ||
| C. | A1:A2=3:1,T1:T2=1:2 | D. | A1:A2=3:1,T1:T2=2:1 |
16. 汽车在行驶过程中对地面的压力过小是不安全的.有一辆质量为1600kg的小汽车驶上圆弧半径为50m的拱桥,g取10m/s2,则( )
汽车在行驶过程中对地面的压力过小是不安全的.有一辆质量为1600kg的小汽车驶上圆弧半径为50m的拱桥,g取10m/s2,则( )
 汽车在行驶过程中对地面的压力过小是不安全的.有一辆质量为1600kg的小汽车驶上圆弧半径为50m的拱桥,g取10m/s2,则( )
汽车在行驶过程中对地面的压力过小是不安全的.有一辆质量为1600kg的小汽车驶上圆弧半径为50m的拱桥,g取10m/s2,则( )| A. | 若汽车以5 m/s的速度通过桥顶,对桥顶的压力为800 N | |
| B. | 若汽车以20 m/s的速度通过桥顶,恰好对桥顶没有压力 | |
| C. | 若汽车过桥的速度一定,拱桥半径越小,汽车越安全 | |
| D. | 若汽车过桥的速度一定,拱桥半径越大,汽车越安全 |
1.氢原子的能级公式为En=-$\frac{{E}_{0}}{{n}^{2}}$(n=1,2,3…),式中E0为已知量.氢原子吸收光子从基态跃迁到第二激发态,氢原子增加的质量为( )
| A. | $\frac{2{E}_{0}}{9{c}^{2}}$ | B. | $\frac{4{E}_{0}}{9{c}^{2}}$ | C. | $\frac{5{E}_{0}}{9{c}^{2}}$ | D. | $\frac{8{E}_{0}}{9{c}^{2}}$ |
 如图所示,足够长的水平传送带静止时在左端做标记点P,将工件放在P点,启动传送带,P点向右做匀加速运动,工件相对传送带发生滑动,经过t1=2s时立即控制传送带,P点做匀减速运动,再经过t2=3s传送带停止运行,测得标记点P通过的距离x0=15m.
如图所示,足够长的水平传送带静止时在左端做标记点P,将工件放在P点,启动传送带,P点向右做匀加速运动,工件相对传送带发生滑动,经过t1=2s时立即控制传送带,P点做匀减速运动,再经过t2=3s传送带停止运行,测得标记点P通过的距离x0=15m. 如图所示,一质量为m=3kg、初速度为5m/s的小滑块(可视为质点),向右滑上一质量为M=2kg的静止在水平面上足够长的滑板,m、M间动摩擦因数为μ1=0.2,滑板与水平面间的动摩擦因数为μ2=0.1,(设最大静摩擦力等于滑动摩擦力).
如图所示,一质量为m=3kg、初速度为5m/s的小滑块(可视为质点),向右滑上一质量为M=2kg的静止在水平面上足够长的滑板,m、M间动摩擦因数为μ1=0.2,滑板与水平面间的动摩擦因数为μ2=0.1,(设最大静摩擦力等于滑动摩擦力).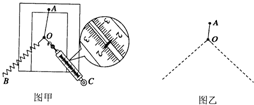 如图甲所示是“探究求共点力合力的方法”
如图甲所示是“探究求共点力合力的方法”