题目内容
1. 如图所示,空间有一水平方向向左的匀强电场,一根非弹性绝缘轻绳一端栓一根质量为m,电量为q的小球,绳子的另一端固定在O点,现把小球拉到使细线水平伸直的位置A,然后将小球静止释放,小球沿圆弧运动到轻绳与水平方向成θ=60°的位置B时速度为0,求
如图所示,空间有一水平方向向左的匀强电场,一根非弹性绝缘轻绳一端栓一根质量为m,电量为q的小球,绳子的另一端固定在O点,现把小球拉到使细线水平伸直的位置A,然后将小球静止释放,小球沿圆弧运动到轻绳与水平方向成θ=60°的位置B时速度为0,求(1)小球所带的电性;
(2)匀强电场的电场强度大小E;
(3)小球运动的整个过程中轻绳的最大拉力F${\;}_{{T}_{m}}$.
分析 类比单摆,小球从A点静止释放,运动到B点速度为0,说明弧AB的中点是运动的最低点,对小球进行受力分析,小球处在弧线中点位置时切线方向合力为零,再根据几何关系可以求出Eq,球到达B点时速度为零,向心力为零,则沿细线方向合力为零,此时对小球受力分析,再根据几何关系即可解题.
解答 解:(1)电场力向右,与场强方向相反,故小球带负电;
(2)类比单摆,根据对称性可知,小球处在弧线中点位置时切线方向合力为零,此时细线与水平方向夹角恰为30°,根据三角函数关系可得:
qEsin30°=mgcos30°,
化简可知:
Eq=$\sqrt{3}$mg,
则E=$\frac{\sqrt{3}mg}{q}$;
(3)小球到达B点时速度为零,根据对称性可知,小球处在弧线中点位置时切线方向合力为零,此时细线与水平方向夹角恰为30°,小球的速度最大,受力分析如图 .
.
该过程中重力与电场力做功,由动能定理得:
$\frac{1}{2}$m${v}_{m}^{2}$-0=mgLsin30°-qEL(1-cos30°)…①
根据牛顿第二定律知:
T-mgsin30°-Eqcos30°=m$\frac{{v}_{m}^{2}}{L}$…②
联立①②解得:T=2mg+(4-2$\sqrt{3}$)mg=6mg+2$\sqrt{3}$mg
答:(1)小球带负电;
(2)匀强电场的电场强度大小E为$\frac{\sqrt{3}mg}{q}$;
(3)小球运动的整个过程中轻绳的最大拉力为6mg+2$\sqrt{3}$mg.
点评 本题要求同学们能正确进行受力,并能联想到已学的物理模型,根据相关公式解题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.雨滴在下降过程中,所受空气阻力与速度的平方成正比,则下列说法中正确的是( )
| A. | 雨滴下落过程中做匀变速运动 | |
| B. | 雨滴下落过程中所受的合外力随速度增大而增大 | |
| C. | 随空气阻力逐渐增大雨滴下落的加速度逐渐减小 | |
| D. | 雨滴下落过程中做自由落体运动 |
16.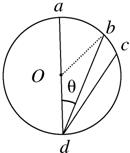 (多选)如图,ad、bd、cd是竖直面内三根固定的光滑细杆,每根杆上套着一个小滑环(图中未画出),三个滑环分别从a、b、c处释放(初速度均为0),用t1、t2、t3依次表示各滑环到达d所用的时间,a1、a2、a3依次表示各滑环的加速度的大小,v1、v2、v3依次表示各滑环到达d的速度大小,则( )
(多选)如图,ad、bd、cd是竖直面内三根固定的光滑细杆,每根杆上套着一个小滑环(图中未画出),三个滑环分别从a、b、c处释放(初速度均为0),用t1、t2、t3依次表示各滑环到达d所用的时间,a1、a2、a3依次表示各滑环的加速度的大小,v1、v2、v3依次表示各滑环到达d的速度大小,则( )
 (多选)如图,ad、bd、cd是竖直面内三根固定的光滑细杆,每根杆上套着一个小滑环(图中未画出),三个滑环分别从a、b、c处释放(初速度均为0),用t1、t2、t3依次表示各滑环到达d所用的时间,a1、a2、a3依次表示各滑环的加速度的大小,v1、v2、v3依次表示各滑环到达d的速度大小,则( )
(多选)如图,ad、bd、cd是竖直面内三根固定的光滑细杆,每根杆上套着一个小滑环(图中未画出),三个滑环分别从a、b、c处释放(初速度均为0),用t1、t2、t3依次表示各滑环到达d所用的时间,a1、a2、a3依次表示各滑环的加速度的大小,v1、v2、v3依次表示各滑环到达d的速度大小,则( )| A. | t1=t2=t3 | B. | t1>t2>t3 | C. | a1>a2>a3 | D. | v1=v2=v3 |
13. 如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )
如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )
 如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )
如图所示,整个空间存在水平向左的匀强电场,一长为L的绝缘轻质细硬杆一端固定在O点,另一端固定一个质量为m、电荷量为+q的小球P,杆可绕O点在竖直平面内无摩擦转动,电场的电场强度大小为E=$\frac{\sqrt{3}mg}{3q}$,先把杆拉成水平,然后将杆无初速度释放、重力加速度为g,不计空气阻力,则( )| A. | 小球到最低点时速度最大 | |
| B. | 小球从开始至最低点过程中动能先增大后减小 | |
| C. | 小球对杆的最大拉力大小为$\frac{8\sqrt{3}}{3}$mg | |
| D. | 小球可绕O点做完整的圆周运动 |
2.质量为m的物体,由静止开始下落,由于阻力的作用,下落的加速度为$\frac{4}{5}$g,在物体下落h的过程中,下列说法正确的是( )
| A. | 物体的动能增加了$\frac{4}{5}$mgh | B. | 物体的机械能减少了$\frac{1}{5}$mgh | ||
| C. | 物体克服阻力做功$\frac{1}{5}$mgh | D. | 物体重力势能减少了$\frac{4}{5}$mgh |
3.电磁学的成就极大地推动了人类社会的进步.下列说法错误的是( )
| A. |  此图中,这是录音机的录音电路原理图,当录音机录音时,由于话筒的声电转换,线圈中变化的电流在磁头缝隙处产生变化的磁场 | |
| B. |  此图电路中,开关断开瞬间,灯泡会突然闪亮一下,并在开关处产生电火花 | |
| C. |  此图中,在真空冶炼中,可以利用高频电流产生的涡流冶炼出高质量的合金 | |
| D. |  此图中,钳形电流表是利用电磁感应原理制成的,它的优点是不需要切断导线,就可以方便地测出通过导线中交变电流的大小 |
 在匀强磁场中(磁感应强度为B)有一折导线abc,ab=bc=L,θ=60°,导线中的电流方向如图所示,电流强度为I,求该折导线受到安培力的大小和方向.
在匀强磁场中(磁感应强度为B)有一折导线abc,ab=bc=L,θ=60°,导线中的电流方向如图所示,电流强度为I,求该折导线受到安培力的大小和方向.