题目内容
11.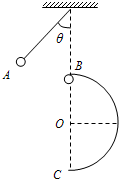 如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到悬点正下方B处线被拉断,紧接着摆球恰好能沿竖直放置的半圆形轨道内侧做圆周运动,已知摆线长l=2.0m,轨道半径R=2.0m,摆球质量m=0.5kg,不计空气阻力.(g取10m/s2)
如图所示,让摆球从图中的A位置由静止开始下摆,正好摆到悬点正下方B处线被拉断,紧接着摆球恰好能沿竖直放置的半圆形轨道内侧做圆周运动,已知摆线长l=2.0m,轨道半径R=2.0m,摆球质量m=0.5kg,不计空气阻力.(g取10m/s2)(1)求摆球在A点时与竖直方向的夹角θ;
(2)若半圆形内侧轨道上有摩擦,已知摆球到达最低点C时的速度为6m/s,求摩擦力做的功.
分析 摆球从C到D的过程机械能守恒,在D点刚好不脱离半圆轨道,说明重力恰好提供向心力;写出两个公式即可求出小球在D点的速度和在C点的夹角;
D到F的过程中重力与摩擦力做功,小球的速度增大.
解答 解:(1)在D点刚好不脱离半圆轨道,有:$mg=m\frac{{{v_D}^2}}{R}$
得:${v_D}=2\sqrt{5}$m/s
从C点到D点机械能守恒,有:$mgL(1-cosθ)=\frac{1}{2}m{v_D}^2$
得:$θ=\frac{π}{3}$
(2)从D点到最低点,由动能定理得:$2mgR+{W_摩}=\frac{1}{2}m{v^2}-\frac{1}{2}m{v_D}^2$
解得:W摩=-16J
答:(1)摆球在C点时与竖直方向的夹角为$\frac{π}{3}$
(2)摩擦力做的功16J.
点评 该题的关键是在D点刚好不脱离半圆轨道,说明重力恰好提供向心力;再根据题意灵活应用动能定理或机械能守恒求解即可.

练习册系列答案
相关题目
19.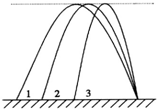 如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
 如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
如图所示,水平地面上不同位置的三个物体沿三条不同的路径抛出,最终落在同一点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )| A. | 沿路径1抛出的物体落地的速率最大 | |
| B. | 沿路径3抛出的物体在空中运动的时间最长 | |
| C. | 沿路径3抛出的物体初速度的竖直分量最大 | |
| D. | 三个物体抛出时初速度的水平分量相等 |
6. 如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直放在光滑的水平面上,木块A上放有质量为2m的木块C,三者均处于静止状态.现将木块C迅速移开,若重力加速度为g,则在木块C移开的瞬间( )
如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直放在光滑的水平面上,木块A上放有质量为2m的木块C,三者均处于静止状态.现将木块C迅速移开,若重力加速度为g,则在木块C移开的瞬间( )
 如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直放在光滑的水平面上,木块A上放有质量为2m的木块C,三者均处于静止状态.现将木块C迅速移开,若重力加速度为g,则在木块C移开的瞬间( )
如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直放在光滑的水平面上,木块A上放有质量为2m的木块C,三者均处于静止状态.现将木块C迅速移开,若重力加速度为g,则在木块C移开的瞬间( )| A. | 弹簧的弹性势能立即减小为0 | B. | 木块A的加速度大小为2g | ||
| C. | 弹簧的弹力大小为mg | D. | 木块B对水平面的压力为2mg |
3. 北京时间2013年12月10日晚上九点二十分,在太空飞行了九天的“嫦娥三号”飞船绕月球飞行,假设月球半径为R,月球表面重力加速度为g0.飞船首先沿距月球表面3R的圆轨道Ⅰ运动.到达P点成功变轨到椭圆轨道Ⅱ,两轨道相交于点P,如图所示.关于“嫦娥三号”飞船,以下说法正确的是( )
北京时间2013年12月10日晚上九点二十分,在太空飞行了九天的“嫦娥三号”飞船绕月球飞行,假设月球半径为R,月球表面重力加速度为g0.飞船首先沿距月球表面3R的圆轨道Ⅰ运动.到达P点成功变轨到椭圆轨道Ⅱ,两轨道相交于点P,如图所示.关于“嫦娥三号”飞船,以下说法正确的是( )
 北京时间2013年12月10日晚上九点二十分,在太空飞行了九天的“嫦娥三号”飞船绕月球飞行,假设月球半径为R,月球表面重力加速度为g0.飞船首先沿距月球表面3R的圆轨道Ⅰ运动.到达P点成功变轨到椭圆轨道Ⅱ,两轨道相交于点P,如图所示.关于“嫦娥三号”飞船,以下说法正确的是( )
北京时间2013年12月10日晚上九点二十分,在太空飞行了九天的“嫦娥三号”飞船绕月球飞行,假设月球半径为R,月球表面重力加速度为g0.飞船首先沿距月球表面3R的圆轨道Ⅰ运动.到达P点成功变轨到椭圆轨道Ⅱ,两轨道相交于点P,如图所示.关于“嫦娥三号”飞船,以下说法正确的是( )| A. | 在轨道Ⅰ上运动到P点的速度比在轨道Ⅱ上运动到P点的速度小 | |
| B. | 在轨道Ⅰ上运行的速率为$\sqrt{{g}_{0}R}$ | |
| C. | 在轨道Ⅰ上的势能与动能之和比在轨道Ⅱ上的势能与动能之和大 | |
| D. | 在轨道Ⅰ上运动的周期小于在轨道Ⅱ上运动的周期 |
 如图所示方格形平面区域,小正方形边长为24m,为方便描述以左下角O点为坐标原点,向东方向建立X轴,向北方向建立Y轴,X轴上连续分布一系列探测器.甲、乙分别操作两辆小车A、B在方形区域运动,当探测器监测到两辆小车有相同的X坐标,立即发出一声且只发出一声报鸣声.设甲操作A车以初速度2.5m/s,加速度0.025m/s2从(0,24)出发向东行驶,乙操作B车由静止开始以加速度0.15m/s2从(24,48)同时出发向东行驶,试问探测器会发出报鸣声吗,如果会,请求出报鸣声发出对应的时刻.
如图所示方格形平面区域,小正方形边长为24m,为方便描述以左下角O点为坐标原点,向东方向建立X轴,向北方向建立Y轴,X轴上连续分布一系列探测器.甲、乙分别操作两辆小车A、B在方形区域运动,当探测器监测到两辆小车有相同的X坐标,立即发出一声且只发出一声报鸣声.设甲操作A车以初速度2.5m/s,加速度0.025m/s2从(0,24)出发向东行驶,乙操作B车由静止开始以加速度0.15m/s2从(24,48)同时出发向东行驶,试问探测器会发出报鸣声吗,如果会,请求出报鸣声发出对应的时刻. 如图在(0,y0)和(0,-y0)两位置分别固定一个电荷量为+Q的点电荷.另一个带电量为+q的点电荷从(-x0,0)位置以初速度v0沿x轴正方向运动.点电荷+q从(-x0,0)到(x0,0)的过程中只受电场力作用,下列描述其加速度a或速度v与位置x的关系可能正确的是( )
如图在(0,y0)和(0,-y0)两位置分别固定一个电荷量为+Q的点电荷.另一个带电量为+q的点电荷从(-x0,0)位置以初速度v0沿x轴正方向运动.点电荷+q从(-x0,0)到(x0,0)的过程中只受电场力作用,下列描述其加速度a或速度v与位置x的关系可能正确的是( )



 轻杆的一端安装有一个小滑轮P,用手握住杆的另一端支撑着悬挂重物的轻绳,如图所示.现使杆和竖直方向的夹角缓慢减小,则下列关于杆对滑轮P的作用力的下列判断正确的是( )
轻杆的一端安装有一个小滑轮P,用手握住杆的另一端支撑着悬挂重物的轻绳,如图所示.现使杆和竖直方向的夹角缓慢减小,则下列关于杆对滑轮P的作用力的下列判断正确的是( )