题目内容
11.一辆汽车在前一半位移内的平均速度为v1,后一半位移内的平均速度为v2,则在整个过程中的平均速度为$\frac{2{v}_{1}{v}_{2}}{{v}_{1}+{v}_{2}}$;如果这辆车在前一半时间内的平均速度为v3,后一半时间内的平均速度为v4,则在整个过程中的平均速度为$\frac{{v}_{3}+{v}_{4}}{2}$.分析 根据平均速度的定义式,结合前一半位移和后一半位移内的时间,求出全程的平均速度.同理可由两段时间内的位移求出平均速度.
解答 解:设全程的位移为x,则平均速度为:
$\overline{v}=\frac{x}{t}=\frac{x}{\frac{\frac{x}{2}}{{v}_{1}}+\frac{\frac{x}{2}}{{v}_{2}}}=\frac{2{v}_{1}{v}_{2}}{{v}_{1}+{v}_{2}}$.
设一半的时间为t;则前一半时间内的位移x1=v3t;后一半时间内的位移x2=v4t;
则平均速度为:$\overline{{v}_{t}}$=$\frac{x}{t}$=$\frac{{v}_{3}t+{v}_{4}t}{2t}$=$\frac{{v}_{3}+{v}_{4}}{2}$;
故答案为:$\frac{2{v}_{1}{v}_{2}}{{v}_{1}+{v}_{2}}$,$\frac{{v}_{3}+{v}_{4}}{2}$
点评 解决本题的关键掌握平均速度的定义式,要根据位移与时间的比值求解平均速度,绝不能都代速度的平均值来计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.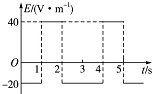 如图所示为匀强电场的电场强度E随时间t变化的图象.当t=0时,在此匀强电场中由静止释放一个带正电的粒子,设带电粒子只受电场力的作用,则下列说法中正确的是( )
如图所示为匀强电场的电场强度E随时间t变化的图象.当t=0时,在此匀强电场中由静止释放一个带正电的粒子,设带电粒子只受电场力的作用,则下列说法中正确的是( )
 如图所示为匀强电场的电场强度E随时间t变化的图象.当t=0时,在此匀强电场中由静止释放一个带正电的粒子,设带电粒子只受电场力的作用,则下列说法中正确的是( )
如图所示为匀强电场的电场强度E随时间t变化的图象.当t=0时,在此匀强电场中由静止释放一个带正电的粒子,设带电粒子只受电场力的作用,则下列说法中正确的是( )| A. | 带电粒子将始终向同一个方向运动 | B. | 2 s末带电粒子回到原出发点 | ||
| C. | 3 s末带电粒子的速度不为零 | D. | 0~3 s内,电场力做的总功为零 |
2.一个矩形线圈在匀强磁场中绕轴匀速转动,产生的感应电动势e=311sin100πt(V),则( )
| A. | 线圈的转速为300r/min | B. | 电动势的有效值为220V | ||
| C. | 当t=$\frac{1}{200}$s时,电动势达最大值 | D. | 当t=0时,线圈平面与中性面垂直 |
6.(多选)下列说法符合历史事实的是( )
| A. | 伽利略通过“理想实验”得出结论:一旦物体具有某一速度,如果它不受力,它将以这一速度永远运动下去 | |
| B. | 牛顿发现了万有引力定律,并测出了万有引力常量G=6.67X10-11N.m2/Kg2 | |
| C. | 牛顿提出了行星运动三大定律 | |
| D. | 库仑发现了电荷间作用的规律,并测出了静电力常量K=9.0X109N.m2/C2 |
16. 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中某两颗工作卫星1和2在同一轨道上绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中某两颗工作卫星1和2在同一轨道上绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )
 北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中某两颗工作卫星1和2在同一轨道上绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )
北斗导航系统又被称为“双星定位系统”,具有导航、定位等功能.“北斗”系统中某两颗工作卫星1和2在同一轨道上绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如图所示.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.以下判断中正确的是( )| A. | 卫星1由位置A运动到位置B的过程中万有引力做正功 | |
| B. | 如果使卫星1加速,它就一定能追上卫星2 | |
| C. | 这两颗卫星所在处的重力加速度大小相等,均为$\frac{Rg}{r}$ | |
| D. | 卫星1由位置A运动至位置B所需的时间为$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$ |
3.下列描述中正确的是( )
| A. | 发生光电效应时入射光波长相同,从金属表面逸出的光电子最大初动能越大,这种金属的逸出功越小 | |
| B. | 当放射性元素的原子的核外电子具有较高能量时,将发生β衰变 | |
| C. | 按照玻尔理论,氢原子核外电子从低能级跃迁到高能级时,电子的动能减少,原子的能量增大 | |
| D. | 放射性的原子核发生衰变后产生的新核从高能级向低能级跃迁时,辐射出γ射线 | |
| E. | 放射性物质放出的射线中,α粒子动能很大,因此贯穿物质的本领很强 |
1.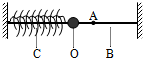 如图所示,弹簧振子在光滑水平杆上B、C两点间做机械振动,O为平衡位置,A为OB间的一个点,则( )
如图所示,弹簧振子在光滑水平杆上B、C两点间做机械振动,O为平衡位置,A为OB间的一个点,则( )
 如图所示,弹簧振子在光滑水平杆上B、C两点间做机械振动,O为平衡位置,A为OB间的一个点,则( )
如图所示,弹簧振子在光滑水平杆上B、C两点间做机械振动,O为平衡位置,A为OB间的一个点,则( )| A. | 振动过程中,弹簧振子的机械能不守恒 | |
| B. | 振子从C到O的过程中,弹簧弹性势能转化为振子动能 | |
| C. | 振子经过位置O时动能为零 | |
| D. | 振子每次经过A点时的动能都不同 |
 如图所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0从斜面的顶端P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0,物块A与斜面间的动摩擦因数为μ,斜面倾角为θ.求:
如图所示,轻弹簧一端固定在与斜面垂直的挡板上,另一端点在O位置.质量为m的物块A(可视为质点)以初速度v0从斜面的顶端P点沿斜面向下运动,与弹簧接触后压缩弹簧,将弹簧右端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0,物块A与斜面间的动摩擦因数为μ,斜面倾角为θ.求: