题目内容
5.一个电子以速度v0垂直进入偏转电场,并能飞出偏转电场,已知两偏转极板间电压为U,要使电子落在极板上而不飞出偏转电场,则应采取的措施是( )| A. | 增大v0,减小U | B. | 增大v0,U不变 | C. | 增大v0,增大U | D. | v0不变,减小U |
分析 电子垂直进入偏转电场后做类平抛运动,把电子的运动分解为垂直于电场方向的匀速直线运动,沿电场方向的初速度为零的匀加速直线运动,由分位移公式得到偏转距离表达式,再分析即可.
解答 解:电子垂直进入偏转电场后做类平抛运动,设两偏转极板的长度为L,两偏转极板间距离为d,则有 L=v0t,得:t=$\frac{L}{{v}_{0}}$;
偏转距离为 y=$\frac{1}{2}$at2,又 a=$\frac{qU}{md}$,得:y=$\frac{qU{L}^{2}}{2md{v}_{0}^{2}}$
要使电子落在极板上而不飞出偏转电场,应使y增大,由上式可知,可采取的措施是:增大v0,增大U,其他方法不行,故ABD错误,C正确.
故选:C
点评 类平抛运动与平抛运动研究的方法相似,把粒子的运动分解成匀速直线运动和匀加速直线运动,结合牛顿第二定律和匀变速直线运动规律解题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
10. 如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )
如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )
 如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )
如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂直于纸面向里的匀强磁场.三个相同带正电的粒子,比荷为$\frac{q}{m}$,先后从A点沿AD方向以大小不等的速度射入匀强磁场区域,粒子在运动过程中只受磁力作用.已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上某一点垂直边界飞出磁场区域.则( )| A. | 编号为①的粒子在磁场区域内运动的时间为$\frac{πm}{qB}$ | |
| B. | 编号为②的粒子在磁场区域内运动的时间为$\frac{πm}{3qB}$ | |
| C. | 三个粒子进入磁场的速度依次减小 | |
| D. | 三个粒子在磁场内运动的时间依次增加 |
17. 如图所示,a、b 分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的 U-I 图象,已知导体电阻R=ρ$\frac{l}{s}$,下列说法正确的是( )
如图所示,a、b 分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的 U-I 图象,已知导体电阻R=ρ$\frac{l}{s}$,下列说法正确的是( )
 如图所示,a、b 分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的 U-I 图象,已知导体电阻R=ρ$\frac{l}{s}$,下列说法正确的是( )
如图所示,a、b 分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的 U-I 图象,已知导体电阻R=ρ$\frac{l}{s}$,下列说法正确的是( )| A. | a 代表的电阻丝较粗 | |
| B. | b 代表的电阻丝较粗 | |
| C. | a 电阻丝的阻值小于 b 电阻丝的阻值 | |
| D. | 图线表示两个电阻丝的电阻随电压的增大而增大 |
15. 某一导体的伏安特性曲线如图中AB段(曲线)所示,曲线上A、B两点的切线分别过(0,0.5)和(0,1.0),关于导体的电阻,以下说法正确的是( )
某一导体的伏安特性曲线如图中AB段(曲线)所示,曲线上A、B两点的切线分别过(0,0.5)和(0,1.0),关于导体的电阻,以下说法正确的是( )
 某一导体的伏安特性曲线如图中AB段(曲线)所示,曲线上A、B两点的切线分别过(0,0.5)和(0,1.0),关于导体的电阻,以下说法正确的是( )
某一导体的伏安特性曲线如图中AB段(曲线)所示,曲线上A、B两点的切线分别过(0,0.5)和(0,1.0),关于导体的电阻,以下说法正确的是( )| A. | B点的电阻为12Ω | |
| B. | B点的电阻为40Ω | |
| C. | 导体的电阻因温度的影响改变了10Ω | |
| D. | 导体的电阻因温度的影响改变了9Ω |
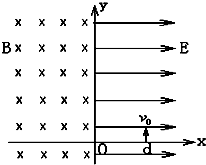 如图所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度E=10N/C;在x<0的空间中,存在垂直xy平面方向的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求:
如图所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度E=10N/C;在x<0的空间中,存在垂直xy平面方向的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求: 如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电荷量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图虚线所示.不计粒子的重力及它们间的相互作用.求
如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电荷量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图虚线所示.不计粒子的重力及它们间的相互作用.求 如图所示,MN、PQ是平行金属板,板长为L,两板间距离为$\frac{1}{2}$L,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场.不计粒子重力.试求:
如图所示,MN、PQ是平行金属板,板长为L,两板间距离为$\frac{1}{2}$L,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场.不计粒子重力.试求: