题目内容
7. 如图所示,质量均为m、电荷量均为q的两带异种电荷的粒子从O点进入边界水平的匀强磁场中,带负电粒子的速度v1=v0,方向与磁场水平边界MN的夹角α=30°,带正电粒子的速度v2=$\sqrt{3}$v0,两粒子速度方向垂直.已知匀强磁场的磁感应强度为B、方向垂直纸面向里,两粒子同时到达磁场边界,不计重力及粒子间相互作用.
如图所示,质量均为m、电荷量均为q的两带异种电荷的粒子从O点进入边界水平的匀强磁场中,带负电粒子的速度v1=v0,方向与磁场水平边界MN的夹角α=30°,带正电粒子的速度v2=$\sqrt{3}$v0,两粒子速度方向垂直.已知匀强磁场的磁感应强度为B、方向垂直纸面向里,两粒子同时到达磁场边界,不计重力及粒子间相互作用.(1)求两粒子在磁场边界上的穿出点间的距离d.
(2)求两粒子进入磁场的时间间隔△t.
(3)若MN下方有平行于纸面的匀强电场,且两粒子出磁场后即在电场中相遇,其中带负电粒子做直线运动.求电场强度E的大小和方向.
分析 (1)作出两粒子的运动轨迹,由牛顿第二定律求出半径,结合几何知识求出d;
(2)根据公式t=$\frac{θ}{2π}$T求运动时间;
(3)由题意,电场强度的方向应与粒子1穿出磁场的方向平行,分为与粒子速度方向相同和相反两种情况进行讨论.
解答 解:(1)粒子在匀强磁场中作匀速圆周运动:
根据牛顿第二定律:qvB=m$\frac{{v}^{2}}{r}$
粒子1圆周运动的圆心角θ1=$\frac{5}{3}$π,OA=2r1sinθ1
粒子2圆周运动的圆心角θ2=$\frac{2}{3}$π,OB=2r2sinθ2
故d=OA+OB=2r1sin30°+2r2sin60°=$\frac{4m{v}_{0}}{qB}$
(2)粒子圆周运动的周期为:T=$\frac{2πr}{v}$
粒子1在匀强磁场中运动的时间为:t1=$\frac{{θ}_{1}}{2π}$T
粒子2在匀强磁场中运动的时间为:t2=$\frac{{θ}_{2}}{2π}$T
所以有:△t=t1-t2=$\frac{πm}{3qB}$
(3)由题意,电场强度的方向应与粒子1穿出磁场的方向平行.
情况一:若电场强度的方向与MN成30°角斜向右上,则粒子1做匀加速直线运动,粒子2做类平抛运动.
Eq=ma
ABcos30°=v1t-$\frac{1}{2}$at2-$\frac{1}{2}$at2
ABsin30°=v2t
解得:E=$\sqrt{3}$Bv0
情况二:若电场强度的方向与MN成30°角斜向左下,则粒子1做匀减速直线运动,粒子2做类平抛运动.
Eq=ma
ABcos30°=v1t-$\frac{1}{2}$at2-$\frac{1}{2}$at2
ABsin30°=v2t
解得:E=-$\sqrt{3}$Bv0,假设不成立,
综上所述,电场强度的大小E=3Bv0,方向与MN成30°角斜向右上.
答:(1)两粒子在磁场边界上的穿出点A、B之间的距离是$\frac{4m{v}_{0}}{Bq}$;
(2)两粒子进入磁场的时间间隔是$\frac{πm}{3qB}$;
(3)若MN下方有平行于纸面的匀强电场,且两粒子在电场中相遇,其中的粒子1做直线运动.电场强度E的大小为$\sqrt{3}$Bv0,方向与MN成30°角斜向右上.
点评 本题考查带电粒子在磁场中和电场中运动的问题,解题关键是要正确画出粒子轨迹过程图,再与几何关系联立,对学生几何能力要求较高,注意第(3)问由于电场的方向不确定,所以存在两种可能的情况,注意分析取舍.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案 如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )
如图所示,B、C、D、E、F五个球并排放置在光滑的水平面上,B、C、D、E四球质量相等,而F球质量小于B球质量,A球的质量等于F球质量,A球以速度v0向B球运动,所发生的碰撞均为弹性碰撞,则碰撞之后( )| A. | 五个小球静止,一个小球运动 | B. | 四个小球静止,两个小球运动 | ||
| C. | 三个小球静止,三个小球运动 | D. | 六个小球都运动 |
 如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )
如图所示,在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场,x轴下方存在垂直纸面向外的磁感应强度为$\frac{B}{2}$的匀强磁场.一带负电的粒子从原点O以与x轴成30°角斜向上射入磁场,且在x轴上方运动的半径为R.不计重力,则( )| A. | 粒子经偏转一定能回到原点O | |
| B. | 粒子在x轴上方和下方两磁场中运动的半径之比为1:2 | |
| C. | 粒子完成一次周期性运动的时间为$\frac{πm}{3qB}$ | |
| D. | 粒子第二次射入x轴上方磁场时,沿x轴前进3R |
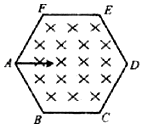 如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂离子纸面向里的匀强磁场.三个带正电的粒子以相同的速度υ先后从A点沿AD方向射入匀强磁场区域.粒子在运动过程中只受磁场力作用,已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上的某一点垂 直边界飞出磁场区域.则下列说法正确的是( )
如图所示,在一个边长为a的正六边形区域内存在磁感应强度为B,方向垂离子纸面向里的匀强磁场.三个带正电的粒子以相同的速度υ先后从A点沿AD方向射入匀强磁场区域.粒子在运动过程中只受磁场力作用,已知编号为①的粒子恰好从F点飞出磁场区域,编号为②的粒子恰好从E点飞出磁场区域,编号为③的粒子从ED边上的某一点垂 直边界飞出磁场区域.则下列说法正确的是( )| A. | 编号为①的粒子的比荷为$\frac{{\sqrt{3}υ}}{Ba}$ | |
| B. | 编号为②的粒子在磁场区域内运动的时间$t=\frac{πm}{6qB}$ | |
| C. | 编号为③的粒子在ED边上飞出的位置与E点的距离(2$\sqrt{3}$-3)a | |
| D. | 三个粒子在磁场内运动的时间依次减少并且为4:2:1 |
| A. | “轨道康复者”的速度是地球同步卫星速度的5倍 | |
| B. | “轨道康复者”的加速度是地球同步卫星加速度的5倍 | |
| C. | 站在赤道上的人可观察到“轨道康复者”向东运动 | |
| D. | “轨道康复者”可在高轨道上加速,以实现对低轨道上卫星的拯救 |
 “橡皮筋动力飞机”比赛是淮安市中小学生科技模型大赛中热门项目之一,如图,一小孩缠绞橡皮筋,使质量为50g的橡皮筋动力飞机由静止上升到约6m的高度处,则在缠绞过程中手对橡皮筋做的功可能是( )
“橡皮筋动力飞机”比赛是淮安市中小学生科技模型大赛中热门项目之一,如图,一小孩缠绞橡皮筋,使质量为50g的橡皮筋动力飞机由静止上升到约6m的高度处,则在缠绞过程中手对橡皮筋做的功可能是( )| A. | 1J | B. | 2J | C. | 2.5J | D. | 4.5J |
 如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别为A、B、C,O′为O在水平面上的投影点,且O′A:O′B:O′C=l:3:5.若不计空气阻力,则下列说法正确的是( )
如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别为A、B、C,O′为O在水平面上的投影点,且O′A:O′B:O′C=l:3:5.若不计空气阻力,则下列说法正确的是( )| A. | v1:v2:v3=5:3:1 | |
| B. | 在C点落地的小球落地时的动能一定最大 | |
| C. | 三个小球落地的速度相同 | |
| D. | 三个小球下落的时间相同 |