题目内容
16. 一固定斜面长为L=12.5m,倾角为θ=30°,斜面动摩擦因数为μ=$\frac{{\sqrt{3}}}{5}$.若用一平行于斜面的恒定外力F=16N,将一个质量为m=1kg的小物体从斜面底端推上斜面顶部,如图所示,求力F作用的最短时间.(g=10m/s2)
一固定斜面长为L=12.5m,倾角为θ=30°,斜面动摩擦因数为μ=$\frac{{\sqrt{3}}}{5}$.若用一平行于斜面的恒定外力F=16N,将一个质量为m=1kg的小物体从斜面底端推上斜面顶部,如图所示,求力F作用的最短时间.(g=10m/s2)
分析 物体在力F的推动下加速上滑,提前撤销,使的物体运动到最高点时,速度恰好减为零,则推力F用时最短;先根据牛顿第二定律求解出加速和减速的加速度,然后根据运动学公式列式求解.
解答 解:要使力F作用最短时间,则物体应在F作用下先匀加速运动时间t1后撤去F,然后做匀减速运动冲上斜面顶部,速度刚好为零.
匀加速运动:${a_1}=\frac{F-mgsinθ-μmgcosθ}{m}$
根据位移时间公式得:${S_1}=\frac{1}{2}{a_1}{t_1}^2$
根据速度时间公式得:v=a1t1
匀减速运动:${a_2}=\frac{mgsinθ+μmgcosθ}{m}$
根据位移时间公式得:${S_2}=\frac{1}{2}{a_2}t_2^2$
根据速度时间公式得:v=a2t2
S1+S2=l
代入数据,联立解得t1=1.25s.
答:求力F作用的最短时间为1.25s.
点评 本题关键是受力分析后根据牛顿第二定律求解出加速度,然后根据运动学公式列式求解.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.额定电压为4V的直流电动机的线圈电阻为1Ω,正常工作时,电动机线圈每秒产生的热量为1J,下列计算结果正确的是( )
| A. | 电动机正常工作时的输入功率为1W | |
| B. | 电动机正常工作时的输出功率为4W | |
| C. | 电动机每秒能将电能转化成4J的机械能 | |
| D. | 电动机正常工作时的电流强度为1A |
7.汽车和自行车在同一平直的公路上做匀速直线运动,汽车速度为10m/s,自行车速度为4m/s,汽车追上自行车后立即刹车做加速度大小为2m/s2的匀减速直线运动,则两车再次相遇所需时间和通过的路程分别为( )
| A. | 6s,24m | B. | 6 s,25 m | C. | 6.25 s,24 m | D. | 6.25 s,25 m |
4. 平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )
平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )
 平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )
平面MN、PQ、ST为三个相互平行的界面,Ⅰ、Ⅱ、Ⅲ为三种不同的介质,平面ST的上表面涂有反射层(光线不能通过).某种单色光线射向界面MN后,发生了一系列的反射和折射现象,光路如图所示.则( )| A. | 当入射角β适当减小时,光线c、d都可能会消失 | |
| B. | 当入射角β适当增大时,光线d可能会消失 | |
| C. | 对于三种介质,光在介质Ⅱ中的传播速度最小 | |
| D. | 出射光线b、c、d不一定平行 |
11.李平同学拉单杠时,两臂平行握住单杠,在他两臂逐渐分开的过程中,某一只手臂的拉力大小变化情况为( )
| A. | 逐渐变大 | B. | 逐渐变小 | C. | 先变小,后变大 | D. | 先变大,后变小 |
5.LED发光二极管技术得到广泛应用,下表为某发光二极管的正向电压U与正向电流I关系的数据.
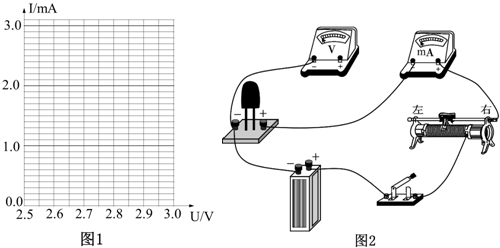
(1)根据以上数据,在图1中画出电压在2.5V〜3.00V范围内二极管的I-U图线.分析曲线可知二极管的电阻随U变大而变小(填‘变大”、“变小”或“不变”),在该范围内电阻最小约为1000Ω;
(2)某同学用伏安法测电阻的电路验证该二极管的伏安特性曲线,要求二极管的正向电压从0开始变化,并使测量误差尽量減小.图2是实验器材实物图,电压表量程为3V,内阻约为3kΩ,电流表量程为5mA,内阻约为10Ω.图中已连接了部分导线,请按实验要求将实物图中的连线补充完整.
(3)若此LED发光二极管的工作电流为2mA,则此发光二极管应与一阻值R=10Ω的电阻串联后才能与电动势为3V、内阻不计的电源相连.
| U/V | 0.00 | 2.56 | 2.71 | 2.80 | 2.84 | 2.87 | 2.89 | 2.91 | 2.99 |
| I/A | 0.00 | 0.03 | 0.07 | 0.11 | 0.34 | 0.52 | 0.75 | 0.91 | 3.02 |

(1)根据以上数据,在图1中画出电压在2.5V〜3.00V范围内二极管的I-U图线.分析曲线可知二极管的电阻随U变大而变小(填‘变大”、“变小”或“不变”),在该范围内电阻最小约为1000Ω;
(2)某同学用伏安法测电阻的电路验证该二极管的伏安特性曲线,要求二极管的正向电压从0开始变化,并使测量误差尽量減小.图2是实验器材实物图,电压表量程为3V,内阻约为3kΩ,电流表量程为5mA,内阻约为10Ω.图中已连接了部分导线,请按实验要求将实物图中的连线补充完整.
(3)若此LED发光二极管的工作电流为2mA,则此发光二极管应与一阻值R=10Ω的电阻串联后才能与电动势为3V、内阻不计的电源相连.
16. 如图所示,通电直导线ab位于两平行导线横截面MN的连线的中垂线上,当平行导线通以同向等值电流时,以下说法中正确的是( )
如图所示,通电直导线ab位于两平行导线横截面MN的连线的中垂线上,当平行导线通以同向等值电流时,以下说法中正确的是( )
 如图所示,通电直导线ab位于两平行导线横截面MN的连线的中垂线上,当平行导线通以同向等值电流时,以下说法中正确的是( )
如图所示,通电直导线ab位于两平行导线横截面MN的连线的中垂线上,当平行导线通以同向等值电流时,以下说法中正确的是( )| A. | 导线ab顺时针旋转 | B. | 导线a端向外,b端向里旋转 | ||
| C. | 导线ab逆时针旋转 | D. | 导线a端向里,b端向外旋转 |

 如图所示,用绳子将重为10N的物体挂在水平横梁上,已知∠BAO=53°,∠ABO=37°.
如图所示,用绳子将重为10N的物体挂在水平横梁上,已知∠BAO=53°,∠ABO=37°.