题目内容
18. 如图所示,在xoy平面内,MN与y轴平行,间距为d,其间有沿x轴负方向的匀强电场.y轴左侧有垂直纸面向外的匀强磁场,磁感应强度大小为B1,MN右侧空间有垂直纸面的匀强磁场,质量为m,电荷量为q的粒子以v0的速度从坐标原点O沿x轴负方向射入磁场,经过一段时间后再次回到坐标原点,粒子在此过程中通过电场的总时间t总=$\frac{4d}{3{v}_{0}}$,粒子重力不计,求:
如图所示,在xoy平面内,MN与y轴平行,间距为d,其间有沿x轴负方向的匀强电场.y轴左侧有垂直纸面向外的匀强磁场,磁感应强度大小为B1,MN右侧空间有垂直纸面的匀强磁场,质量为m,电荷量为q的粒子以v0的速度从坐标原点O沿x轴负方向射入磁场,经过一段时间后再次回到坐标原点,粒子在此过程中通过电场的总时间t总=$\frac{4d}{3{v}_{0}}$,粒子重力不计,求:(1)左侧磁场区域的最小宽度
(2)电场区域电场强度的大小
(3)右侧磁场区域宽度及磁感应强度满足的条件.
分析 (1)临界情况是左侧磁场区域的左边界与轨迹相切,根据牛顿第二定律列式求解轨道半径,得到左侧磁场区域的最小宽度;
(2)粒子在电场中运动的时间已知的,根据匀变速直线运动的速度公式列式求解加速度,根据牛顿第二定律列式求解电场强度;
(3)临界情况是经过右侧磁场偏转后在电场中沿着直线回到O点,也可以是在左侧磁场中再运动半圈回到O点,结合几何关系求解轨道半径,根据牛顿第二定律列式求解即可.
解答 解:(1)粒子在磁场做圆周运动(半圈)
由$q{B}_{1}{v}_{0}=m\frac{{v}_{0}^{2}}{R}$
轨道半径:R=$\frac{m{v}_{0}}{q{B}_{1}}$
由几何知识可知,左侧磁场的最小宽度就是粒子做圆周运动的半径
即${L}_{min}=R=\frac{m{v}_{0}}{q{B}_{1}}$
(2)粒子在电场中来回的总时间为${t}_{总}=\frac{4d}{3{v}_{0}}$,所以电场对带电粒子单次通过的时间为t=$\frac{2d}{3{v}_{0}}$,显然,粒子首次通过电场中是加速运动,粒子应该带负电.
由$d={v}_{0}t+\frac{1}{2}a{t}^{2}$
即$d={v}_{0}t+\frac{1}{2}\frac{qE}{m}{t}^{2}$
得到:E=$\frac{3m{v}_{0}^{2}}{2qd}$
(3)粒子在左侧磁场中向下偏转,通过电场加速后进入右侧磁场,要使其能够回到原点,在右侧磁场中应向下偏转,且偏转半径为R或2R,粒子加速通过电场加速后进入右侧磁场速度为v.
根据速度公式,有:
v=v0+at=2v0
根据牛顿第二定律,有:
qvB=m$\frac{{v}^{2}}{r}$
解得:
r=$\frac{mv}{qB}$=$\frac{2m{v}_{0}}{qB}$
R=$\frac{m{v}_{0}}{q{B}_{1}}$
①当半径r=R时,则B=$\frac{2m{v}_{0}}{qR}$=2B1
右侧磁场的最小宽度为${X}_{min}=R=\frac{m{v}_{0}}{q{B}_{1}}$
②当半径r=2R时,B=$\frac{2m{v}_{0}}{qR}$=B1
右侧磁场的最小宽度为${X}_{min}=r=\frac{2m{v}_{0}}{q{B}_{1}}$
答:(1)左侧磁场区域的最小宽度为$\frac{m{v}_{0}}{q{B}_{1}}$;
(2)电场区域电场强度的大小为$\frac{3m{v}_{0}^{2}}{2qd}$;
(3)右侧磁场区域宽度及磁感应强度满足的条件为:①B=2B1,${X}_{min}=\frac{m{v}_{0}}{q{B}_{1}}$;②B=B1,${X}_{min}=\frac{2m{v}_{0}}{q{B}_{1}}$.
点评 本题关键是明确粒子的受力情况和运动规律,找到临界情况,然后根据牛顿第二定律、运动学公式并结合几何关系列式分析,不难.

 口算能手系列答案
口算能手系列答案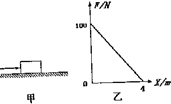 如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )
如图甲所示,在水平地面上放置一个质量为m=4kg的物体,让其在随位移均匀减小的水平推力作用下运动,推力随位移x变化的图象乙所示,已知物体与底面间的动摩擦因数μ=0.5,g=10m/s2,下列说法正确的是( )| A. | 物体先做加速运动,推力撤去时开始做减速运动 | |
| B. | 物体在水平面上运动的最大位移是10m | |
| C. | 物体运动的最大速度为2$\sqrt{15}$m/s | |
| D. | 物体在运动中的加速度先变小后不变 |
| A. | 飞船运动的周期变大 | B. | 飞船运动的角速度变大 | ||
| C. | 飞船运动的速率变小 | D. | 飞船运动的向心加速度变小 |
| A. | 北斗-G1的绕地运行周期大于北斗-M6的绕地运行周期 | |
| B. | 北斗-G1的绕地运行速率大于北斗-M6的绕地运行速率 | |
| C. | 北斗-G1的绕地运行的向心加速度大于北斗-M6的绕地运行向心加速度 | |
| D. | 北斗-G1只能在赤道的正上方 |
| A. | 月球绕O点转动的角速度减小 | B. | 月球绕O点转动的角速度增大 | ||
| C. | 地球球心到O点的距离减小 | D. | 月球绕O点转动的动能增加 |
 如图所示,有三个斜面a、b、c,底边的长分别为L、L、3L,高度分别为3h、h、h.某物体与三个斜面间的动摩擦因数都相同,这个物体分别沿三个斜面从顶端由静止下滑到底端.三种情况相比较,下列说法正确的是( )
如图所示,有三个斜面a、b、c,底边的长分别为L、L、3L,高度分别为3h、h、h.某物体与三个斜面间的动摩擦因数都相同,这个物体分别沿三个斜面从顶端由静止下滑到底端.三种情况相比较,下列说法正确的是( )| A. | 物体损失的机械能2△Ec=2△Eb=4△Ea | |
| B. | 因摩擦产生的热量3Qa=3Qb=Qc | |
| C. | 物体到达底端的动能Eka=3Ekb=3Ekc | |
| D. | 因摩擦产生的热量4Qa=2Qb=Qc |
 根据波尔原子结构理论,氦离子(He+)的能级图如图所示,当某个He+处在n=4的激发态时,由于跃迁所发射的谱线可能有几条( )
根据波尔原子结构理论,氦离子(He+)的能级图如图所示,当某个He+处在n=4的激发态时,由于跃迁所发射的谱线可能有几条( )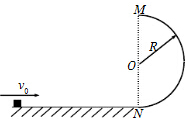 如图,质量m=1.0kg的物体(可视为质点)以v0=10m/s的初速度从水平面的某点向右运动并冲上半径R=1.0m的竖直光滑半圆环,物体与水平面间的动摩擦因数μ=0.5.求:
如图,质量m=1.0kg的物体(可视为质点)以v0=10m/s的初速度从水平面的某点向右运动并冲上半径R=1.0m的竖直光滑半圆环,物体与水平面间的动摩擦因数μ=0.5.求: