��Ŀ����
16����ͼ���ھ�����ΪH=0.5m�Ĺ⻬���������һ�̶���ֱ�壬���Ϲ̶�һ���ɣ�����������һ��ܱ��ij�ΪL=0.5m��ľ�壬ľ�����˹̶�����ֱ���壨��ľ��һ���˶�����ľ��õ����������ΪM=2kg����ľ���Ͻ����������һ����Ϊm=1kg��Сľ�飬Сľ����ľ��֮���Ħ������Ϊ��=0.1���������Ҷ˹̶���һ�ܰ���ճ�壬��߶��Ե��ڳ�ľ��ĺ�ȣ�����ľ��ײ��ճ����ʱ���ٶ�������Ϊ0���ھ������Ҷ�S=1m����һ��Ϊh=0.3m��ˮƽ����ΪL0=0.2m�ĵ������ó�ľ�彫����ѹ��������ϸ���̶����������Ҷ��볤ľ�岻ճ������ľ���Ҷ˾������Ҷ��㹻Զ��g=10m/s2�� ���ն����ӣ���ľ���Сľ��һ�𱻵���������1��������Сľ��ͣ�ڳ�ľ�����Ҷˣ����ն���ʱ���ɴ���ĵ��������Ƕ��
��2����ҪʹСľ���������ڵ����ϣ��ɵĵ�����������ʲô��Χ�ڣ�

���� ��1����ľ��Mײ��ճ���m��M���������ȼ����˶�����ϵ��ɴ���ĵ������ܵ���m��M�ij�ʼ���ܼ�����ȷ��⣮
��2��������뿪������ٶȣ��پ�ƽ���˶�֪ʶ�Ͷ��ܶ�����⼴�ɣ�
��� �⣺
��1�����ɵ�����m��Mһ������������ֱ���˶������ٶȴ�СΪ v0��Mײ��ճ���m��M���������ȼ����˶������뿪M���ɶ��ܶ����У�
$0-\frac{1}{2}m{v}_{0}^{2}=-��mgL$
���ԣ�${v}_{0}^{2}=2��gL$
���ɴ���ĵ������ܵ���m��M�ij�ʼ���ܣ�����
${E}_{P}=\frac{1}{2}��M+m��{v}_{0}^{2}=�̣�M+m��gL$
�������ݵã�EP=1.5J
��2����m�պ��������ĵˣ�m�뿪ľ�����ƽ���˶��ij��ٶ�Ϊv1�����У�
$H=\frac{1}{2}g{t}_{1}^{2}$
S=v1t1
���ԣ�${v}_{1}=S\sqrt{\frac{g}{2H}}$
�������ݵã�${v}_{1}=\sqrt{10}$m/s
���ɵ���ʱ��m��M���ٶ�Ϊvmin����m��M���˶��Ĺ����У�
$\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}_{min}^{2}=-��mgL$
���ԣ�${v}_{min}^{2}={v}_{1}^{2}+2��gL$
���ɵĵ���������СֵΪ��EPmin=16.5J
��m�պ��������Ķ��ˣ���$H-h=\frac{1}{2}g{t}_{2}^{2}$
S+L=${v}_{2}{t}_{2}^{2}$
���ԣ�${v}_{2}=��S+{L}_{0}��•\sqrt{\frac{g}{2��H-h��}}=6$m/s
��ʱ���ɵ���ʱ��m��M���ٶ�Ϊvmax����m��M���˶��Ĺ����У�
$\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{max}^{2}=-��mgL$
���ɵĵ����������ֵΪ��EPmax=55.5J
���ԣ����ɵ�������Ӧ�����з�Χ�ڣ�16.5J��EP��55.5J
�𣺣�1��������Сľ��ͣ�ڳ�ľ�����Ҷˣ����ն���ʱ���ɴ���ĵ���������1.5J
��2����ҪʹСľ���������ڵ����ϣ��ɵĵ�������������16.5J��EP��55.5J��
���� �������ڵ��������̵��������ȷ��������˶�����ǽ���Ĺؼ������Ӧ�ö��ܶ������˶�ѧ��ʽ��ƽ���˶���֪ʶ�ǽ���Ĺؼ��������˶����̽ϸ��ӣ��ѶȽϴ�

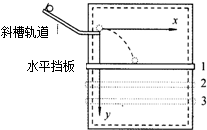 ij����ʵ��С�������ͼ��ʾ��װ���о�ƽ���˶���ÿ�ζ���С���б�۵�ͬһλ�������ͷţ�����б��ĩ��ˮƽ�ɳ����ı�ˮƽ����ĸ߶ȣ��ı���С���ڰ�������λ�ã��Ӷ�������С����˶��켣��ijͬѧ��������ʵ�飬��ˮƽ�������η���1��2��3��λ�ã���l��2�ļ�����2��3�ļ�࣮������ʵ���У�С����׳��㵽����ˮƽλ������Ϊxl��x2��x3�����Կ���������Ӱ�죬���������ȷ���ǣ�������
ij����ʵ��С�������ͼ��ʾ��װ���о�ƽ���˶���ÿ�ζ���С���б�۵�ͬһλ�������ͷţ�����б��ĩ��ˮƽ�ɳ����ı�ˮƽ����ĸ߶ȣ��ı���С���ڰ�������λ�ã��Ӷ�������С����˶��켣��ijͬѧ��������ʵ�飬��ˮƽ�������η���1��2��3��λ�ã���l��2�ļ�����2��3�ļ�࣮������ʵ���У�С����׳��㵽����ˮƽλ������Ϊxl��x2��x3�����Կ���������Ӱ�죬���������ȷ���ǣ�������| A�� | x2-xl��x3-x2 | B�� | x2-xl=x3-x2 | C�� | x2-xl��x3-x2 | D�� | ���ж� |
| A�� | С�α����ʾ�����ĵ�����Ť�Ӳ�����������Ϳ�����Ť���о����֮����������������˷Ŵ� | |
| B�� | ٤����Ӧ������ʵ��˵������ά�������˶���ԭ�� | |
| C�� | ˲ʱ�ٶȶ��塢˲ʱ���ٶȶ���Ӧ���˼��� | |
| D�� | ���Ƶ��ȱ���ֱ���˶�λ�ƹ�ʽʱ���������˶����̻��ֳɺܶ�С�Σ�ÿһС�ν��ƿ�������ֱ���˶���Ȼ���ø�С�ε�λ��֮�ʹ��������λ��Ӧ����Ԫ�� |
 ��ͼ��A��B������������ͬ�Ĺ���뾶�ֱ�������ΪM��3M������������Բ���˶�������˵����ȷ���ǣ�������
��ͼ��A��B������������ͬ�Ĺ���뾶�ֱ�������ΪM��3M������������Բ���˶�������˵����ȷ���ǣ�������| A�� | ����A�Ľ��ٶȱ�B�� | B�� | ����A�����ٶȱ�BС | ||
| C�� | ����A�����ļ��ٶȱ�B�Ĵ� | D�� | ����A���������ڱ�B��С |
| A�� | ���칬һ�š��������ٶȱ�ͬ�����ǵĿ� | |
| B�� | ���칬һ�š����ܵ���������ͬ�����ǵ�С | |
| C�� | ���칬һ�š������ļ��ٶȱ�ͬ�����ǵĴ� | |
| D�� | ���칬һ�š����������ڱ�ͬ�����ǵ�С |
| A�� | 2P | B�� | 4P | C�� | 8P | D�� | 16P |
 ��ͼ��ʾ��һ������ӿ�����ֱ���䵽ֱ�����⾵��BC���ϣ���֪��A=30�㣬�⾵��������ٽ��Ϊ45�㣬������
��ͼ��ʾ��һ������ӿ�����ֱ���䵽ֱ�����⾵��BC���ϣ���֪��A=30�㣬�⾵��������ٽ��Ϊ45�㣬������| A�� | ��ֱ�����⾵�������������Ϊ$\sqrt{2}$ | |
| B�� | ��ֱ�����⾵�������������Ϊ$\frac{\sqrt{2}}{2}$ | |
| C�� | �����һ�δ��⾵�������ʱ�������Ϊ45�� | |
| D�� | �����һ�δ��⾵�������ʱ�������Ϊ60�� |
 ͼ��������桰�ļ�����Ϸ����ʵ��Ƭ����ҽ�һ����ΪAB�ĵ������ӵ�һ��ϵ�����ϣ���һ�˹̶��ڸߴ���Ȼ��Ӹߴ����£�ͼ������ҵ�����͵�ʱ�����������ABΪ�������ӵ�ԭ����C���ǵ�������������λ�ã�D����������������͵㣬��������뿪��̨����͵�Ĺ����У�����˵����ȷ���ǣ�������
ͼ��������桰�ļ�����Ϸ����ʵ��Ƭ����ҽ�һ����ΪAB�ĵ������ӵ�һ��ϵ�����ϣ���һ�˹̶��ڸߴ���Ȼ��Ӹߴ����£�ͼ������ҵ�����͵�ʱ�����������ABΪ�������ӵ�ԭ����C���ǵ�������������λ�ã�D����������������͵㣬��������뿪��̨����͵�Ĺ����У�����˵����ȷ���ǣ�������| A�� | ��������һֱ������ | |
| B�� | �����D����ٶ�Ϊ0 | |
| C�� | ���ͨ��B��֮�����Ӿ��е������� | |
| D�� | �����B���ٶ���� |
 ��ͼ��ʾ������ֱƽ�������Ű뾶ΪR�⻬��$\frac{1}{4}$Բ���ۣ�����ĩ��ˮƽ��������H��һ��С���A���ɾ�ֹ��ʼ�»�����B���ˮƽ�ɳ������ƿ�����������֪С������m���������ٶ�Ϊ g����
��ͼ��ʾ������ֱƽ�������Ű뾶ΪR�⻬��$\frac{1}{4}$Բ���ۣ�����ĩ��ˮƽ��������H��һ��С���A���ɾ�ֹ��ʼ�»�����B���ˮƽ�ɳ������ƿ�����������֪С������m���������ٶ�Ϊ g����