题目内容
11．
如图，在水平固定放置的气缸内，用不漏气的轻质活塞封闭有一定量的理想气体，开有小孔的薄隔板将气体分为A、B两部分．活塞的横截面积为S，与气缸壁之间无摩擦．初始时A、B两部分容积相同，温度为T，大气压强为p0．（1）加热气体，使A、B两部分体积之比达到1：2，求此时的温度T′；
（2）将气体温度加热至2T，然后在活塞上施加一向左的水平恒力F=5p0S，推动活塞，直至最终达到平衡，推动活塞过程中温度始终维持2T不变，求最终气体压强p?．
分析 （1）已知初末状态的体积，由盖吕萨克定律可求得后来的温度；
（2）由理想气体状态方程可求得临界压强值，比值临界压强与压力压强的关系，可分析活塞的位置，进而求得最终的压强．
解答 解：
（1）设A的容积为V，则初状态AB总体积2V，末状态总体积3V
等压变化 $\frac{2V}{T}$=$\frac{3V}{T′}$
解得T?=1.5T
（2）假设活塞推至隔板时气体压强为p临
$\frac{{P}_{0}×2V}{T}$=$\frac{{P}_{临}V}{2T}$
解得p临=4p0＜$\frac{F}{s}$
由此可以判断，活塞一直被推至隔板，此后气体压强不再改变，p′=4p0
答：（1）温度为1.5T；
（2）最终气体压强为4P0．
点评 本题考查理想气体的状态方程的应用，在解题时要注意临界条件的正确应用，明确物体对应的状态．
练习册系列答案
相关题目
用如图的电路可以精确测量定值电阻R0的电阻值和滑动变阻器R2的总阻值，图中R1为电阻箱，主要操作步骤如下，完成步骤中的填空：
小明在研究性学习中设计了一种可测量磁感应强度的实验，其装置如图所示．在该实验中，磁铁固定在水平放置的电子测力计上，此时电子测力计的读数为G1，磁铁两极之间的磁场可视为水平匀强磁场，其余区域磁场不计．直铜条AB的两端通过导线与一电阻连接成闭合回路，总阻值为R．若让铜条水平且垂直于磁场，以恒定的速率v在磁场中竖直向下运动，这时电子测力计的读数为G2，铜条在磁场中的长度L．则铜条匀速运动时所受安培力的方向是竖直向上，大小是G2-G1，磁感应强度的大小是$\frac{1}{L}\sqrt{\frac{（{G}_{2}-{G}_{1}）R}{v}}$．
19．
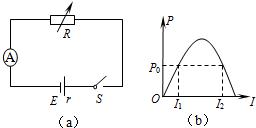如图（a），R为电阻箱，A为理想电流表，电源的电动势为E，内阻为r．图（b）为电源的输出功率P与A示数I的关系图象，其中功率P0分别对应电流I1、I2．则（ ）
如图（a），R为电阻箱，A为理想电流表，电源的电动势为E，内阻为r．图（b）为电源的输出功率P与A示数I的关系图象，其中功率P0分别对应电流I1、I2．则（ ）| A． | I1+I2＞$\frac{E}{r}$ | B． | I1+I2＜$\frac{E}{r}$ | C． | I1+I2=$\frac{E}{r}$ | D． | I1=I2=$\frac{E}{r}$ |
16．质量不等的两星体在相互间的万有引力作用下，绕两者连线上某一定点O做匀速圆周运动，构成双星系统．由天文观察测得其运动周期为T两星体之间的距离为r，已知引力常量为G．下列说法正确的是（ ）
| A． | 双星系统的平均密度为$\frac{3π}{{G{T^2}}}$ | |
| B． | O点离质量较大的星体较远 | |
| C． | 双星系统的总质量为$\frac{{4{π^2}{r^3}}}{{G{T^2}}}$ | |
| D． | 若在O点放一物体，则物体受两星体的万有引力合力为零 |
如图所示，两平行的光滑金属导轨安装在一倾角为α的光滑绝缘斜面上，导轨间距为L，电阻忽略不计且足够长，以宽度为d的有界匀强磁场垂直于斜面向上，磁感应强度为B．另有一长为2d的绝缘杆将一导体棒和一边长为d（d＜L）的正方形线框连在一起组成的固定装置，总质量为m，导体棒中通有大小恒为I的电流．将整个装置置于导轨上，开始时导体棒恰好位于磁场的下边界处．由静止释放后装置沿斜面向上运动，当线框的下边运动到磁场的上边界MN处时装置的速度恰好为零．重力加速度为g．
12．关于地球同步卫星，它们具有相同的（ ）
| A． | 质量 | B． | 高度 | C． | 向心力 | D． | 周期 |