题目内容
11．在空间某一点以大小相等的速度分别竖直上抛、竖直下抛、水平抛出质量相等的小球，不计空气阻力，则从抛出到落地的总时间内（ ）| A． | 做下抛运动的小球动量变化最大 | B． | 做平抛运动的小球动量变化最小 | ||
| C． | 三个小球动量变化大小相等 | D． | 三个小球动量变化率相等 |
分析 根据动量定理，动量该变量等于合力的冲量，只有重力做功，故运动时间长的动量改变量大；根据动量定理，动量的变化率等于合力．
解答 解：ABC、三个球运动过程中只受重力作用，根据动量定理，动量改变量等于合力的冲量，故动量的改变量等于重力的冲量；
上抛运动的时间最长，下抛运动的时间最短，根据△P=I=mgt，做上抛运动的小球动量变化最大，做下抛运动的小球动量变化最小；
故A错误，B错误，C错误；
D、根据动量定理，动量的变化率等于合力，合力相等，故三个球的动量的变化率相等，故D正确；
故选：D
点评 本题考查动量定理，关键是知道动量的改变量大小等于合力的冲量，动量变化率等于合力，不难．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
1．
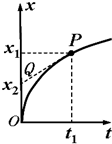如图所示是一做匀变速直线运动的质点的位置-时间图象（x-t图象），P（t1，x1）为图象上一点．PQ为过P点的切线，与x轴交于点Q．则下列说法正确的是（ ）
如图所示是一做匀变速直线运动的质点的位置-时间图象（x-t图象），P（t1，x1）为图象上一点．PQ为过P点的切线，与x轴交于点Q．则下列说法正确的是（ ）| A． | t1时刻，质点的速率为$\frac{{x}_{1}}{{t}_{1}}$ | |
| B． | t1时刻，质点的速率为$\frac{{x}_{1}-{x}_{2}}{{t}_{1}}$ | |
| C． | 质点的加速度大小为$\frac{{x}_{1}-{x}_{2}}{{t}_{1}^{2}}$ | |
| D． | 0-t1时间内，质点的平均速度大小为$\frac{2（{x}_{1}-{x}_{2}）}{{t}_{1}}$ |
2．
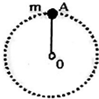长度为0.5m的轻质细杆OA，A端有一质量为3kg的小球，以O为圆心，在竖直平面内做圆周运动，如图所示，小球通过最高点时的速度为2m/s，取g=10m/s2，则此时轻杆OA将（ ）
长度为0.5m的轻质细杆OA，A端有一质量为3kg的小球，以O为圆心，在竖直平面内做圆周运动，如图所示，小球通过最高点时的速度为2m/s，取g=10m/s2，则此时轻杆OA将（ ）| A． | 受到6.0N的拉力 | B． | 受到24N的拉力 | C． | 受到6.0N的压力 | D． | 受到54N的拉力 |
6．在“研究平行板电容器的电容与哪些因素有关”的实验中，用电容表可以直接测量出该平行板电容器的电容大小．某同学在测量中，记录了一些测量结果，参看表，表中的数据是测量出的电容大小．在实验误差的允许范围内，可以得到的最直接的结论是（ ）
| 实验次数 | 极板材质 | 介质材料 | 正对面积 | |||
| S | $\frac{3}{4}s$ | $\frac{1}{2}s$ | $\frac{1}{4}s$ | |||
| ① | 铜 | 橡胶 | 680pF | 530pF | 380pF | 230pF |
| ② | 铁 | 橡胶 | 660pF | 520pF | 380pF | 240pF |
| ③ | 铝 | 亚克力板 | 330pF | 280pF | 230pF | 160pF |
| A． | 通过①和②数据，可知极板材料不影响平行板电容器的电容 | |
| B． | 通过①和③数据，可知极板材料和介质材料都影响平行板电容器的电容 | |
| C． | 通过②和③数据，可知介质材料影响平行板电容器的电容 | |
| D． | 通过①、②和③数据，可知极板的不同正对面积影响平行板电容器的电容 |
16．
如图所示，等腰直角斜臂A的直角边靠在粗糙的竖直墙壁上，一根不可伸长的轻绳一端固定在竖直墙上，另一端与半径不可忽略的光滑球B连接，轻绳与水平方向成30°角，现将轻绳上端点沿竖直墙缓缓向上移动，A始终处于静止状态，则（ ）
如图所示，等腰直角斜臂A的直角边靠在粗糙的竖直墙壁上，一根不可伸长的轻绳一端固定在竖直墙上，另一端与半径不可忽略的光滑球B连接，轻绳与水平方向成30°角，现将轻绳上端点沿竖直墙缓缓向上移动，A始终处于静止状态，则（ ）| A． | 绳上拉力逐渐增大 | B． | 竖直墙对A的摩擦力先减小后增大 | ||
| C． | 竖直墙对A的摩擦力可能为零 | D． | 竖直墙对A的支持力逐渐减小 |
如图所示，某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动，将螺丝帽套在塑料管上，手握塑料管使其保持竖直并沿水平方向做半径为r的匀速圆周运动，则只要运动角速度大小合适，螺丝帽恰好不下滑．假设螺丝帽与塑料管间的动摩擦因数为μ，认为最大静摩擦力近似等于滑动摩擦力．则在该同学手转动塑料管使螺丝帽恰好不下滑时，则此时手转动塑料管的角速度ω=$\sqrt{\frac{g}{μr}}$，若杆的转动加快，螺丝帽不可能（填“可能”“不可能”）与杆发生相对运动．