题目内容
 长为l的轻杆一端固定一个质量为m的小球,以另一端为固定的转动轴,使之在竖直平面内做圆周运动,求以下两种情况中小球在最高点的速度各为多少?
长为l的轻杆一端固定一个质量为m的小球,以另一端为固定的转动轴,使之在竖直平面内做圆周运动,求以下两种情况中小球在最高点的速度各为多少?(1)在最高点时,若小球对杆的压力为
| 1 |
| 2 |
(2)在最高点时,若小球对杆的拉力为
| 1 |
| 2 |
分析:小球通过最高点时,受重力和杆的弹力作用,杆的弹力和重力和合力提供向心力,根据牛顿第二定律求解.
解答:解:(1)在最高点,根据牛顿第二定律得:
对小球有:mg-F=m
,
由题意,F=
mg
所以:v=
(2)在最高点,根据牛顿第二定律得:
对小球有:F+mg=m
,所以:v=
答:(1)在最高点时,若小球对杆的压力为
mg,小球在最高点的速度为
.
(2)在最高点时,若小球对杆的拉力为
mg.小球在最高点的速度为
.
对小球有:mg-F=m
| v2 |
| l |
由题意,F=
| 1 |
| 2 |
所以:v=
|
(2)在最高点,根据牛顿第二定律得:
对小球有:F+mg=m
| v2 |
| l |
|
答:(1)在最高点时,若小球对杆的压力为
| 1 |
| 2 |
|
(2)在最高点时,若小球对杆的拉力为
| 1 |
| 2 |
|
点评:解答竖直平面内圆周运动的问题,关键通过分析受力,确定向心力的来源,运用牛顿第二定律求解.

练习册系列答案
相关题目
 如图所示,长为L的轻杆一端固定质量为m的小球,另一端可绕固定转轴0无摩擦转动.静止在最低点P的小球瞬间获得一水平初速度后在竖直面内做完整的圆周运动,Q为最高点.则以下说法正确的是( )
如图所示,长为L的轻杆一端固定质量为m的小球,另一端可绕固定转轴0无摩擦转动.静止在最低点P的小球瞬间获得一水平初速度后在竖直面内做完整的圆周运动,Q为最高点.则以下说法正确的是( )| A、小球通过P点时处于平衡状态 | B、小球在P点时可能对轻杆有向上的压力作用 | C、小球在Q点时可能对轻杆没有作用力 | D、轻杆在小球通过Q点时对小球的作用力一定小于轻杆在小球通过p点时对小球 的作用力 |
 长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动.现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为
长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动.现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点,若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点,若小球通过圆周轨道最低点时的速度大小为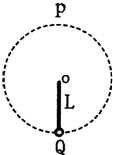 如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定转动轴O,杆可在竖直平面内绕轴O无摩擦地转动.已知小球通过最高点P时,速度的大小为
如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定转动轴O,杆可在竖直平面内绕轴O无摩擦地转动.已知小球通过最高点P时,速度的大小为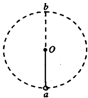 如图所示,长为L 的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,b为圆周运动的最高点.若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L 的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,b为圆周运动的最高点.若小球通过圆周轨道最低点时的速度大小为