题目内容
15. 如图所示,光滑水平地面上有一质量M=5kg、足够长的木板,以v0=10m/s的初速度沿水平地面向右运动.在长木板的上方安装一个固定挡板PQ(挡板靠近但不接触长木板),当长木板的最右端到达挡板正下方时,立即将质量m=1kg的小铁块贴着挡板的左侧无初速地放在长木板上,铁块与长木板之间的动摩擦因数μ=0.5.当木板向右运动s=1m时,又无初速地贴着挡板在第1个小铁块上放置第2个相同的小铁块,以后每当长木板向右运动s=1m就在铁块的上方再放置一个相同的小铁块,直到长木板停止运动(放到木板上的各个铁块始终被挡板挡住而保持静止状态).求:
如图所示,光滑水平地面上有一质量M=5kg、足够长的木板,以v0=10m/s的初速度沿水平地面向右运动.在长木板的上方安装一个固定挡板PQ(挡板靠近但不接触长木板),当长木板的最右端到达挡板正下方时,立即将质量m=1kg的小铁块贴着挡板的左侧无初速地放在长木板上,铁块与长木板之间的动摩擦因数μ=0.5.当木板向右运动s=1m时,又无初速地贴着挡板在第1个小铁块上放置第2个相同的小铁块,以后每当长木板向右运动s=1m就在铁块的上方再放置一个相同的小铁块,直到长木板停止运动(放到木板上的各个铁块始终被挡板挡住而保持静止状态).求:(1)第1个铁块放上后,木板的加速度;
(2)放置第3个铁块的瞬间,长木板的速度;
(3)长木板上最终叠放了多少个铁块?
分析 (1)根据牛顿第二定律求出第1个铁块放上后,木板的加速度.
(2)根据速度位移公式求出放上第二个铁块时的速度,结合牛顿第二定律求出放置第2个铁块后的加速度,从而结合速度位移公式求出放置第3个铁块的瞬间,长木板的速度.
(3)长木板停下来前,结合动能定理,通过摩擦力做功求出放上铁块的个数.
解答 解:(1)牛顿第二定律:-μmg=Ma1
a1=$\frac{-μmg}{M}=\frac{-0.5×10}{5}m/{s}^{2}$=-1m/s2,方向向左
(2)放置第2个铁块瞬间长木板的速度为v1,
由$2{a_1}s={v}_1^2-{v}_0^2$,解出v1=$\sqrt{{v}_0^2+2{a_1}s}$
代入数据解得v1=$\sqrt{98}$m/s
放置第2个铁块后,牛顿第二定律:-2μmg=Ma2
a2=-$\frac{2μmg}{M}=\frac{-2×0.5×10}{5}m/{s}^{2}$=-2m/s2
由$2{a_2}s={v}_2^2-{v}_1^2$,解出放置第3个铁块瞬间长木板的速度
v2=$\sqrt{{v}_1^2+2{a_2}s}$
代入数据解得v2=$\sqrt{94}$m/s
(3)长木板停下来之前,由动能定理得:
∑Wf=0-$\frac{1}{2}M{v}_0^2$
而∑Wf=(-μmgs)+(-2μmgs)+…(-nμmgs)=-$\frac{(1+n)n}{2}$μmgs
解出n=9.5,
所以最终应有10个铁块放在长木板上.
答:(1)第1个铁块放上后,木板的加速度为1m/s2,方向向左;
(2)放置第3个铁块的瞬间,长木板的速度为$\sqrt{94}$m/s;
(3)长木板上最终叠放了10个铁块.
点评 本题考查了动能定理、牛顿第二定律和运动学公式的综合运用,理清铁块和木板的运动规律,选择合适的规律进行求解,难度中等.

 如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力分别推A和B,它们均静止不动,则 ( )
如图所示,质量为m的木块A放在质量为M的三角形斜劈上,现用大小均为F、方向相反的水平力分别推A和B,它们均静止不动,则 ( )| A. | 地面对B的支持力大小一定等于(M+m)g | |
| B. | B与地面之间一定存在摩擦力 | |
| C. | B对A的支持力一定小于mg | |
| D. | A与B之间一定存在摩擦力 |
 如图所示,一个由绝缘材料做成的曲线环水平放置,OAB为环的对称轴,A点位于环内,B点位于环外.在A、B两点分别固定两个点电荷QA和QB,已知A点固定的电荷为正电荷,一个带正电的小球P穿在环上,可沿环无摩擦滑动.给小球P以一定的初始速度,小球恰好沿环匀速率运动,下列判断中正确的是( )
如图所示,一个由绝缘材料做成的曲线环水平放置,OAB为环的对称轴,A点位于环内,B点位于环外.在A、B两点分别固定两个点电荷QA和QB,已知A点固定的电荷为正电荷,一个带正电的小球P穿在环上,可沿环无摩擦滑动.给小球P以一定的初始速度,小球恰好沿环匀速率运动,下列判断中正确的是( )| A. | B点固定的电荷QB一定为正电荷 | |
| B. | B点固定的电荷QB一定为负电荷 | |
| C. | QA和QB产生的电场,在环上的电场强度处处相等 | |
| D. | QA和QB产生的电场,在环上的电势处处相等 |
| A. | 电饭煲 | B. | 电话机 | C. | 复印机 | D. | 电冰箱 |
| A. | 0.2g | B. | 0.4g | C. | 2.5g | D. | 5g |
| A. | 给汽车轮胎充气时费力说明分子间有斥力 | |
| B. | 液体很难被压缩说明液体分子间只存在斥力 | |
| C. | 给气球充气时,需要用力,这说明分子间有斥力 | |
| D. | 以上说法都不正确 |

 如图所示,两个质量均为m、带电量均为+q的小球A和B,固定在轻质绝缘等腰直角三角形框架OAB的两个端点上,直角边的长度为L,另一端点用光滑铰链固定在O点,整个装置可以绕经过O点、且垂直于纸面的水平轴在竖直平面内自由转动.若在竖直平面内施加平行于框架的匀强电场,为使框架静止时OB边水平、OA边竖直(A在O点的正下方),则场强E的大小至少为$\frac{\sqrt{2}mg}{2q}$.若匀强电场的方向竖直向上,场强大小为E′=$\frac{7mg}{q}$,并将A球的带电量改为-q,其余条件不变,将系统从图示位置由静止释放,则小球A的最大速度为$\sqrt{2gL}$.
如图所示,两个质量均为m、带电量均为+q的小球A和B,固定在轻质绝缘等腰直角三角形框架OAB的两个端点上,直角边的长度为L,另一端点用光滑铰链固定在O点,整个装置可以绕经过O点、且垂直于纸面的水平轴在竖直平面内自由转动.若在竖直平面内施加平行于框架的匀强电场,为使框架静止时OB边水平、OA边竖直(A在O点的正下方),则场强E的大小至少为$\frac{\sqrt{2}mg}{2q}$.若匀强电场的方向竖直向上,场强大小为E′=$\frac{7mg}{q}$,并将A球的带电量改为-q,其余条件不变,将系统从图示位置由静止释放,则小球A的最大速度为$\sqrt{2gL}$.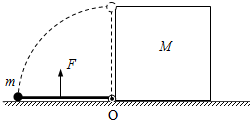 如图,长为L的轻杆一端连着质量为m的小球,另一端与固定于地面上O点的铰链相连,初始时小球静止于地面上,边长为L、质量为M的正方体左侧紧靠O点.现在杆中点处施加一个方向始终垂直杆、大小$\frac{12mg}{π}$的力F,经过一段时间后撤去F,小球恰好能到达最高点,不计一切摩擦.求:
如图,长为L的轻杆一端连着质量为m的小球,另一端与固定于地面上O点的铰链相连,初始时小球静止于地面上,边长为L、质量为M的正方体左侧紧靠O点.现在杆中点处施加一个方向始终垂直杆、大小$\frac{12mg}{π}$的力F,经过一段时间后撤去F,小球恰好能到达最高点,不计一切摩擦.求: