��Ŀ����
5�� ��ͼ��ʾ�����������ڴ��ڴ�ֱֽ�������С�ɵ�����ǿ�ų�������Ϊm������Ϊ+q�����ӿ��ڻ���������Բ���˶���P��QΪ�������Ŀ���С�ļ��壬������������Ϊ�㣬ÿ�����ӷ���P��ʱ��P����Ʊ�Ϊ+U��Q������Ա���Ϊ�㣬������P��Q�����õ����٣�ÿ�������뿪Q��ʱ��P�����������Ϊ�㣬�����������糡һ�δμ����¶��ܲ���������t=0ʱ�̣����Ӿ�ֹ��P���С�״����ڵ糡�����¼��٣������Ӿ���P��Q�����ʱ�伫�̣�Ϊʹ����ʼ�ձ����ڰ뾶ΪR��Բ������˶��������B-tͼ������ͼ�л������������ڴŸ�Ӧǿ����ʱ��ı仯��ͼ��˵�����ݣ���ע�⣺��ͼ�б����ͼ�ĵ�λ����������ת4Ȧ�����дŸ�Ӧǿ����ʱ��仯��������ɣ�
��ͼ��ʾ�����������ڴ��ڴ�ֱֽ�������С�ɵ�����ǿ�ų�������Ϊm������Ϊ+q�����ӿ��ڻ���������Բ���˶���P��QΪ�������Ŀ���С�ļ��壬������������Ϊ�㣬ÿ�����ӷ���P��ʱ��P����Ʊ�Ϊ+U��Q������Ա���Ϊ�㣬������P��Q�����õ����٣�ÿ�������뿪Q��ʱ��P�����������Ϊ�㣬�����������糡һ�δμ����¶��ܲ���������t=0ʱ�̣����Ӿ�ֹ��P���С�״����ڵ糡�����¼��٣������Ӿ���P��Q�����ʱ�伫�̣�Ϊʹ����ʼ�ձ����ڰ뾶ΪR��Բ������˶��������B-tͼ������ͼ�л������������ڴŸ�Ӧǿ����ʱ��ı仯��ͼ��˵�����ݣ���ע�⣺��ͼ�б����ͼ�ĵ�λ����������ת4Ȧ�����дŸ�Ӧǿ����ʱ��仯��������ɣ�
���� ����ÿתһ�ܣ��ٶ�����һ�㣬�ɰ뾶��ʽ$r=\frac{mv}{qB}$֪����Ҫʹ�뾶���䣬��Ÿ�Ӧǿ��ҲҪ���ӣ��������ڹ�ʽ$T=\frac{2��m}{qB}$֪�����Ÿ�Ӧǿ�����ӣ������ڽ���С�������ڶ��Է�����Ҫ�����ĸ������ڵ�B-tͼ����Ҫ���ɰ뾶��ʽ�����һ�����ڵĴŸ�Ӧǿ��B1�����ɶ��ܶ�������ڶ��μ���ʱ���ٶȣ����ɰ뾶��ʽ���B2�������ڹ�ʽ����ڶ�Ȧ��ʱ�䣬������ƴӶ����B3��B4 �͵���Ȧ�͵���Ȧ��ʱ�䣮
���  �⣺����һ����PQ�����ʱ���ݶ��ܶ�����
�⣺����һ����PQ�����ʱ���ݶ��ܶ�����
$Uq=\frac{1}{2}m{{v}_{1}}^{2}$����
��һ��������Բ���˶�ʱ����ţ�ٵڶ����ɵã�
$q{v}_{1}{B}_{1}=\frac{m{v}^{2}}{R}$����
ת��һȦ��ʱ�䣺
${t}_{1}=\frac{2��R}{{v}_{1}}$����
������ã�${B}_{1}=\frac{1}{R}\sqrt{\frac{2Um}{q}}$ ${t}_{1}=2��R\sqrt{\frac{m}{Uq}}$
ͬ�������ڶ�����PQ�����ʱ��
$Uq=\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$����
�ڶ���������Բ���˶�ʱ��
$q{v}_{2}{B}_{2}=\frac{m{{v}_{2}}^{2}}{R}$����
����ʱ��Ϊ��${t}_{2}=\frac{2��{R}_{2}}{{v}_{2}}$����
������ã�${B}_{2}=\frac{1}{R}\sqrt{\frac{4Um}{q}}$ ${t}_{2}=2��R\sqrt{\frac{m}{4Uq}}$
������Ƶõ���${B}_{3}=\frac{1}{R}\sqrt{\frac{6Um}{q}}$ ${t}_{3}=2��R\sqrt{\frac{m}{6Uq}}$
${B}_{4}=\frac{1}{R}\sqrt{\frac{8Um}{q}}$ ${t}_{4}=2��R\sqrt{\frac{m}{8Uq}}$
���������������Կ�����${B}_{1}��{B}_{2}��{B}_{3}��{B}_{4}=1��\sqrt{2}��\sqrt{3}��2$
${t}_{1}��{t}_{2}��{t}_{3}��{t}_{4}=4\sqrt{3}��2\sqrt{3}��2\sqrt{2}��\sqrt{6}$
��Ȼ�У�B4=2B1 ${t}_{2}=\frac{1}{2}{t}_{1}$
���Ի�����B-tͼ������ͼ��ʾ��
���� ����Ĺؼ������ڴӵ�һ�μ��١�ת�����ڶ��μ��١�ת��ʱ��Ӧ�ö��ܶ�����ţ�ٵڶ����ɼ��˶�ѧ���ɣ����B��t����ʽ�Ĺ��ɣ��Ӷ�����������κ͵��Ĵμ��١�ת��ʱB��t ����ʽ��

 ��У����ϵ�д�
��У����ϵ�д����о�����ʮһ���͡��칬���Խӹ���ʱ������ʮһ���͡��칬������Ϊ�ʵ�
������������״�ʹ�С�����о������������ػ��Ҫ����ʱ���Ϳɰ����忴���ʵ�
�ۡ������ڰ����д��С�������Ϊ�ο�ϵ
��ֻ�о�ֹ�����������Ϊ�ο�ϵ��
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
 ��ͼ��ʾ����������Ϊd��ƽ�а��������һ��Դ���ӣ�����S�պϣ��������������Ϊm�������Ϊq������ֹ������������������ȷ���ǣ�������
��ͼ��ʾ����������Ϊd��ƽ�а��������һ��Դ���ӣ�����S�պϣ��������������Ϊm�������Ϊq������ֹ������������������ȷ���ǣ�������| A�� | �������� | |
| B�� | ��Դ�綯�ƵĴ�С����$\frac{mgd}{q}$ | |
| C�� | �Ͽ�����S�����������������˶� | |
| D�� | ���ֿ���S�պϣ��ѵ������������ľ����������������������˶� |
 ��ͼ��ʾ��ˮƽ����Ϸ�����ֱ���ϵ���ǿ�糡��ˮƽ���Ͼ�ֹ�Ŵ���Ե���Ĵ��������飬�ڲ����ǵ��������С���ɼ�Ŀ���������£�����һ����Ϊm��������СΪq�ĵ���С�����ٶȦ�ˮƽ����糡��Ȼ��ˮƽ���ٵ�����鷢����ײ������ԭ���ʷ��أ����غ���ں��������������������˶������뿪�糡����֪�������ٶ�Ϊg��������˵����ȷ���ǣ�������
��ͼ��ʾ��ˮƽ����Ϸ�����ֱ���ϵ���ǿ�糡��ˮƽ���Ͼ�ֹ�Ŵ���Ե���Ĵ��������飬�ڲ����ǵ��������С���ɼ�Ŀ���������£�����һ����Ϊm��������СΪq�ĵ���С�����ٶȦ�ˮƽ����糡��Ȼ��ˮƽ���ٵ�����鷢����ײ������ԭ���ʷ��أ����غ���ں��������������������˶������뿪�糡����֪�������ٶ�Ϊg��������˵����ȷ���ǣ�������| A�� | С������磬������������ | B�� | ��ǿ�糡�ij�ǿ��СΪ$\frac{mg}{q}$ | ||
| C�� | С���ڵ糡�����ص�ʱ����� | D�� | ���غ����߹켣��һ���������� |
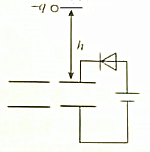 ��ͼ��ʾ��ƽ�а������ˮƽ���ã���Դͨ�������ܸ����ݳ�磬�ϡ��¼���������һС�ף�����Ϊm�������Ϊ-q��С���С�����Ϸ���h���ɾ�ֹ��ʼ���䣬����С�����¼���С�״��ٶ�ǡΪ�㣨�����������Բ��ƣ������糡����Ϊ��ǿ�糡�������ϼ����������ƶ���������
��ͼ��ʾ��ƽ�а������ˮƽ���ã���Դͨ�������ܸ����ݳ�磬�ϡ��¼���������һС�ף�����Ϊm�������Ϊ-q��С���С�����Ϸ���h���ɾ�ֹ��ʼ���䣬����С�����¼���С�״��ٶ�ǡΪ�㣨�����������Բ��ƣ������糡����Ϊ��ǿ�糡�������ϼ����������ƶ���������| A�� | �����ϼ����������ƶ�����С���¼���С�״��ٶ�ǡΪ�� | |
| B�� | �����ϼ����������ƶ�����С���¼���С�״��ٶ�ǡΪ�� | |
| C�� | �����¼����������ƶ�����С���¼���С�״��ٶȾ���Ϊ�� | |
| D�� | �����¼����������ƶ�����С���¼���С�״��ٶ�ǡΪ�� |
| A�� | �ڲ���Ҫ�������屾���Ĵ�С����״ʱ�����ʵ�����������ķ��������˼��跨 | |
| B�� | �����ٶȵĶ���ʽv=$\frac{��x}{��t}$������t��������ʱ���Ϳ��Ա�ʾ������tʱ�̵�˲ʱ�ٶȣ��ö���������Ԫ�� | |
| C�� | ��ʵ��̽�����ٶ������������Ĺ�ϵʱ�������˿��Ʊ����� | |
| D�� | ���Ƶ��ȱ���ֱ���˶�λ�ƹ�ʽʱ���������˶����̵ȷֳɺܶ�С�Σ�Ȼ��С��λ����ӣ�������Ԫ�� |
 ��ͼA��B��ƽ�з��ã������м����һ�����Ե�С�ף�B��ӵأ�A��ĵ��Ʊ仯��ͼ��ʾ�����ֵΪU��������Ϊd������Ӵ�A����С�����ٶȵĽ���糡������t=$\frac{T}{4}$���ڽ���ĵ��ӣ�ǡ���ܵ���B�壮
��ͼA��B��ƽ�з��ã������м����һ�����Ե�С�ף�B��ӵأ�A��ĵ��Ʊ仯��ͼ��ʾ�����ֵΪU��������Ϊd������Ӵ�A����С�����ٶȵĽ���糡������t=$\frac{T}{4}$���ڽ���ĵ��ӣ�ǡ���ܵ���B�壮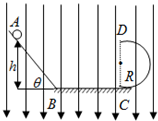 ��ͼ��ʾ������ֱ���µ�����ǿ�糡����һ��Ϲ����һ������С��Ӿ�ˮƽ��Ϊh�Ĺ⻬б�����ϵ�A���ɾ�ֹ�ͷţ���ǿ�糡�ĵ糡ǿ�ȴ�СΪE������С�������Ϊm�������Ϊ-q���⻬б���������Ϊ�ȣ�����С���˶���B��ʱ��������ģ�ˮƽ���BC�dz�ΪL�Ĵֲ�ˮƽ�棬��뾶ΪR�Ĵ�����ֱƽ���ڵĹ⻬��Բ�ι��������C�㣬DΪ��Բ�ι������ߵ㣬����С��ǡ��ͨ�������ߵ�D��С��������������ܵĵ糡�����������ٶ�Ϊg����
��ͼ��ʾ������ֱ���µ�����ǿ�糡����һ��Ϲ����һ������С��Ӿ�ˮƽ��Ϊh�Ĺ⻬б�����ϵ�A���ɾ�ֹ�ͷţ���ǿ�糡�ĵ糡ǿ�ȴ�СΪE������С�������Ϊm�������Ϊ-q���⻬б���������Ϊ�ȣ�����С���˶���B��ʱ��������ģ�ˮƽ���BC�dz�ΪL�Ĵֲ�ˮƽ�棬��뾶ΪR�Ĵ�����ֱƽ���ڵĹ⻬��Բ�ι��������C�㣬DΪ��Բ�ι������ߵ㣬����С��ǡ��ͨ�������ߵ�D��С��������������ܵĵ糡�����������ٶ�Ϊg���� ��ͼ��ʾ���Ը���Ȧ����ɺ��ԣ��պϿ���S��·�ȶ���ͬ����������С����A1��A2���������⣬Ȼ��Ͽ����أ�
��ͼ��ʾ���Ը���Ȧ����ɺ��ԣ��պϿ���S��·�ȶ���ͬ����������С����A1��A2���������⣬Ȼ��Ͽ����أ�