题目内容
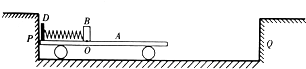
20．
如图所示，质量为m、半径为R的小球，放在半径为2R、质量为2m的大空心球内，大球开始静止在光滑的水平面上，当小球从图示位置无初速度地沿大球内壁滚到最低点时，大球移动的距离是多少？
分析 小球无初速下滑到达最低点时，小球与大球组成的系统水平方向动量守恒，用位移表示平均速度，根据水平方向平均动量守恒定律求出小球发生的水平位移，再由几何知识求出大球的位移．
解答 解：设小球滑到最低点所用的时间为t，发生的水平位移大小为R-x，大球的位移大小为x，取水平向左方向为正方向．则根据水平方向平均动量守恒得：
m$\overline{{v}_{1}}$-2m$\overline{{v}_{2}}$=0
即：m$\frac{R-x}{t}$=2m$\frac{x}{t}$
解得：x=$\frac{R}{3}$
答：大球移动的距离是$\frac{R}{3}$．
点评 本题不能静止地看问题，把圆环当作不动的，要注意位移的参考系．中等难度．
练习册系列答案
百分学生作业本题练王系列答案
互动课堂系列答案
相关题目
10．下列说法中正确的是（ ）
| A． | 匀速圆周运动是一种速度保持不变的运动 | |
| B． | 物体做匀速圆周运动时所受的合外力是恒力 | |
| C． | 作匀速圆周运动的物体的受的合外力为零 | |
| D． | 匀速圆周运动的合力方向始终指向圆心 |
如图所示，一截面为梯形的鱼塘贮满水，鱼塘右侧坡面的倾角为α，水的折射率为n．不同时刻太阳光线与水平面的夹角θ在变化，求当θ满足什么条件时，阳光能够照射到整个鱼塘的底部．
8．
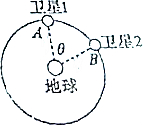2015年3月30日，我国成功发射一颗北斗导航卫星．这是我国发射的第17颗北斗导航卫星，这次成功发射，标志着北斗导航系统由区域运行开始向全球组网．如图所示，北斗导航系统中的两颗地球同步卫星1、2轨道半径均为r，某时刻分别位于轨道上的A、B两个位置，若卫星均沿顺时针方向运行，地球表面的重力加速为g，地球半径为R，不计卫星间的相互作用力，下列判断正确的是（ ）
2015年3月30日，我国成功发射一颗北斗导航卫星．这是我国发射的第17颗北斗导航卫星，这次成功发射，标志着北斗导航系统由区域运行开始向全球组网．如图所示，北斗导航系统中的两颗地球同步卫星1、2轨道半径均为r，某时刻分别位于轨道上的A、B两个位置，若卫星均沿顺时针方向运行，地球表面的重力加速为g，地球半径为R，不计卫星间的相互作用力，下列判断正确的是（ ）| A． | 卫星1向后喷气就一定能够追上卫星2 | |
| B． | 两卫星及其各部分均处于完全失重状态 | |
| C． | 这两颗卫星的线速度大小相等，均为$\sqrt{\frac{GM}{r}}$ | |
| D． | 卫星1由A位置石动到B位置所需的时间是$\frac{θ}{R}$$\sqrt{\frac{{r}^{3}}{g}}$ |
15．
如图所示，一定质量的理想气体由状态a沿直线ab变化到状态b，在此过程中下列说法不正确的是（ ）
如图所示，一定质量的理想气体由状态a沿直线ab变化到状态b，在此过程中下列说法不正确的是（ ）| A． | 气体的温度保持不变 | B． | 气体的密度不断减小 | ||
| C． | 气体对外界做功 | D． | 气体的压强不断减小 |
质谱仪是一种精密仪器，是测量带电粒子的质量和分析同位素的重要工具，从粒子源S产生粒子束（初速度可视为零），经电势差为U的加速电场加速后，垂直进入磁感应强度为B的匀强磁场，粒子束中一个电荷量为+q的粒子经匀强磁场，最终垂直打在记录它照相底片上的P点，测得P点到粒子进入磁场处的距离为l，粒子所受重力不计，求：
真空区域有宽度为L、磁感应强度为B的匀强磁场，磁场方向如图所示，MN、PQ是磁场的边界．质量为m、电荷量为+q的粒子沿着与MN夹角为θ=60°的方向垂直射入磁场中，粒子不能从PQ边界射出磁场（不计粒子重力的影响），求：
如图为一个测温装置，图中C为测温泡，装入水银的U形管B管开口向上，A管通过细玻璃管与测温泡C相通，U形管的下端通过软管相连．测温时，调节B管的高度，使A管中的液面保持在a处，此时根据U形管A、B两管水银面的高度差就能知道测温泡所处环境的温度．假设该测温装置在制定刻度时的大气压为76cmHg，该温度计的0℃和30℃刻度线间的距离正好是30cm．