题目内容
15. 如图所示为某一皮带传动装置.主动轮的半径为r1,从动轮的半径为r2.已知主动轮做顺时针转动,转速为n,转动过程中皮带不打滑,M,N分别是主动轮和从动轮边缘上的一点,则下列说法正确的是( )
如图所示为某一皮带传动装置.主动轮的半径为r1,从动轮的半径为r2.已知主动轮做顺时针转动,转速为n,转动过程中皮带不打滑,M,N分别是主动轮和从动轮边缘上的一点,则下列说法正确的是( )| A. | 角速度ωM:ωN=r2:r1 | B. | 从动轮的转速为$n\frac{r_2}{r_1}$ | ||
| C. | 从动轮做顺时针转动 | D. | 向心加速度aM:aN=r1:r2 |
分析 因为主动轮做顺时针转动,从动轮通过皮带的摩擦力带动转动,所以从动轮逆时针转动,由于通过皮带传动,皮带与轮边缘接触处的线速度相等,根据角速度与线速度的关系即可求解.
解答 解:A、由于通过皮带传动,皮带与轮边缘接触处的线速度相等;由v=ωr,所以:ωM:ωN=r2:r1.故A正确;
B、根据v=2πnr得:n2r2=nr1
所以n2=$n•\frac{{r}_{1}}{{r}_{2}}$.故B错误.
C、因为主动轮做顺时针转动,从动轮通过皮带的摩擦力带动转动,所以从动轮逆时针转动,故C错误;
D、皮带与轮边缘接触处的线速度相等,由:${a}_{n}=\frac{{v}^{2}}{r}$,所以:$\frac{{a}_{M}}{{a}_{N}}=\frac{{r}_{2}}{{r}_{1}}$.故D错误.
故选:A
点评 本题考查了圆周运动角速度与线速度的关系,要知道同一根带子转动,线速度相等,同轴转动,角速度相等.

练习册系列答案
相关题目
5.关于自由落体运动,下列说法正确的是( )
| A. | 物体竖直向下的运动一定是自由落体运动 | |
| B. | 自由落体运动是初速度为零、加速度为g的竖直向下的匀加速直线运动 | |
| C. | 物体下落过程中,速度和加速度同时增大 | |
| D. | 当空气阻力的作用比较小、可以忽略不计时,物体自由下落可视为自由落体运动 |
6.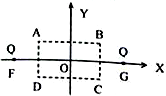 如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )
如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )
 如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )
如图所示,在X轴上关于O点对称的F、G两点有等量同种电荷Q,XOY平面内有一长方形ABCD区域,其中心在O点,AB边与X轴平行,则下列判断正确的是( )| A. | O点电势最高 | |
| B. | A、C两点电场强度相同 | |
| C. | B、D两点电势相等 | |
| D. | 若将点电荷-q从A点移向C,电势能减小 |
3.一个物体做匀速圆周运动,在运动过程中一定不发生变化的物理量是( )
| A. | 向心力 | B. | 线速度 | C. | 角速度 | D. | 向心加速度 |
10.下列说法正确的是( )
| A. | “地心说”是错误的,“日心说”是对的,太阳是宇宙的中心. | |
| B. | 离太阳越近的行星,公转周期越大. | |
| C. | 由开普勒定律知,各行星都有近日点和远日点,且在近日点运动的快,在远日点运动的慢. | |
| D. | 太阳对行星引力的大小与行星的质量成正比,与行星和太阳间的距离成反比. |
7. 如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )
如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )
 如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )
如图所示,某同学通过滑轮将一重物匀速拉升一定高度,不计滑轮与绳的重力及摩擦.重物上升的过程中,下列说法正确的是( )| A. | 人对绳子的拉力保持不变 | B. | 人拉的绳子端点匀速下降 | ||
| C. | 人拉的绳子端点加速下降 | D. | 人对绳子做功的功率保持不变 |
17. 如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )
如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )
 如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )
如图所示,A、B、C三个一样的滑块从粗糙固定斜面上的同一高度同时开始运动,A由静止释放,B的初速度方向沿斜面向下,大小为v0,C的初速度方向沿斜面水平,大小也为v0,下列说法中正确的是( )| A. | A、B、C三者的加速度相同 | B. | 三者中A、C将同时滑到斜面底端 | ||
| C. | 滑到斜面底端时,B的速度最大 | D. | 三者的位移大小相同 |
 质量可以忽略的杆,其长L=2m.其下端固定于O点,上端连接着一个质量m=2kg的小球A,小球绕O点做圆周运动,当经过最高点时,试分别讨论在下列两种情况杆对球的作用力.(计算大小,并说明是拉力还是支持力),g取10 m/s2.
质量可以忽略的杆,其长L=2m.其下端固定于O点,上端连接着一个质量m=2kg的小球A,小球绕O点做圆周运动,当经过最高点时,试分别讨论在下列两种情况杆对球的作用力.(计算大小,并说明是拉力还是支持力),g取10 m/s2. 有一小船正在渡河,如图所示,在到达离对岸30m的P点时,其下游40m处有一危险水域,船的发动机可以使船在静水中以6m/s的速度行驶,假若水流速度为5m/s,求:
有一小船正在渡河,如图所示,在到达离对岸30m的P点时,其下游40m处有一危险水域,船的发动机可以使船在静水中以6m/s的速度行驶,假若水流速度为5m/s,求: