题目内容
14.某兴趣小组的同学利用如图1所示的实验装置,测量木块与长木板之间的动摩擦因数,图中长木板水平固定.
①实验过程中,打点计时器应接在交流(填“直流”或“交流”)电源上,调整定滑轮的高度,使细线与木板平行.
②已知重力加速度为g,测得木块的质量为M,砝码盘和砝码的总质量为m,砝码盘、砝码和木块的加速度大小为a,则木块与长木板之间的动摩擦因数μ=$\frac{mg-(m+M)a}{Mg}$.
③实验时,某同学得到一条纸带,如图2所示,每隔三个计时点取一个计数点,即为图中0、1、2、3、4、5、6点.测得每两个计数点间的距离为s1=0.96cm,s2=2.88cm,s3=4.80cm,s4=6.72cm,s5=8.64cm,s6=10.56cm,打点计时器的电源频率为50Hz.计算此纸带的加速度大小a=3.0m/s2,打第4个计数点时纸带的速度大小v=0.96m/s.(保留两位有效数字)

分析 电火花打点计时器应使用交流电源;对木块、砝码盘和砝码进行受力分析,运用牛顿第二定律求出木块与长木板间动摩擦因数.根据在匀变速直线匀速中时间中点的瞬时速度大小等于该过程中的平均速度大小可以求出某点的瞬时速度大小;利用逐差法可以求出小车的加速度大小
解答 解:(1)电火花计时器应接在交流电源上.细线与长木板平行.
(2)对木块、砝码盘和砝码组成的系统,由牛顿第二定律得:
mg-μMg=(M+m)a,
解得:$μ=\frac{mg-(m+M)a}{Mg}$
每隔三个计时点取一个计数点,所以相邻的计数点之间的时间间隔为T=0.02×4=0.08s
根据△x=aT2,有:
a=$a=\frac{{s}_{6}+{s}_{5}+{s}_{4}-{s}_{3}-{s}_{2}-{s}_{1}}{9{T}^{2}}$=3.0m/s2
在匀变速直线匀速中时间中点的瞬时速度大小等于该过程中的平均速度大小,故有:
v4=$\frac{{s}_{4}+{s}_{5}}{2T}$=0.96m/s.
故答案为:(1)交流;(2)$\frac{mg-(m+M)a}{Mg}$.(3)3.0;0.96
点评 要知道打点计时器的结构、工作原理、使用注意事项,正确选择研究对象,应用牛顿第二定律即可求出动摩擦因数.对于纸带问题的处理,我们要熟悉匀变速直线运动的特点和一些规律,提高应用基本规律解答实验问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列关于氢原子光谱的叙述中正确的是( )
| A. | 从光谱上看,氢原子辐射光波的频率只有若干分立的值 | |
| B. | 稀薄氢气通电时能发出连续谱 | |
| C. | 氢原子从低能级问高能级跃迁时产生原子光谱 | |
| D. | 氢原子从高能级向低能级跃迁时产生原子光谱 |
2.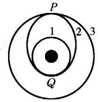 如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示),则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( )
如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示),则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( )
 如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示),则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( )
如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示),则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( )| A. | 卫星在轨道3上的速度大于在轨道1上的速度 | |
| B. | 卫星在轨道3上的角速度小于在轨道1上的角速率 | |
| C. | 卫星在轨道2上经过Q点时的速度大于它在轨道2上经过P点时的速度 | |
| D. | 卫星在轨道1上经过Q点时的加速度小于它在轨道2上经过Q点时的加速度 |
19.假设太阳系中天体的密度不变,天体直径和天体之间距离都缩小到原来的一半,地球绕太阳公转近似为匀速圆周运动,则下列物理量变化正确的是( )
| A. | 地球的向心力变为缩小前的一半 | |
| B. | 地球的向心力变为缩小前的$\frac{1}{16}$ | |
| C. | 地球绕太阳公转周期变为缩小前的$\frac{1}{4}$ | |
| D. | 地球绕太阳公转周期不变 |
6.一行星围绕恒星做圆周运动,并且测得行星的轨道半径和运动周期,由此我们可以推算出( )
| A. | 恒星的质量 | B. | 行星的质量 | C. | 行星的半径 | D. | 恒星的半径 |
3.在勇气号火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来.假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为v0.计算时不计火星大气阻力.已知火星的一个卫星的圆轨道的半径为r,周期为T.火星可视为半径为r0的均匀球体,则它第二次落到火星表面时速度v的大小为( )
| A. | $\sqrt{\frac{8{π}^{2}h{r}^{3}}{{T}^{2}}\frac{{r}^{3}}{{{r}_{0}}^{2}}+{{v}_{0}}^{2}}$ | B. | $\sqrt{\frac{4{π}^{2}h}{{T}^{2}}\frac{r}{{{r}_{0}}^{2}}+{{v}_{0}}^{2}}$ | ||
| C. | $\sqrt{\frac{2{π}^{2}h}{{T}^{2}}\frac{r}{{{r}_{0}}^{2}}}$+v0 | D. | $\sqrt{\frac{2{π}^{2}h}{{T}^{2}}\frac{{r}^{3}}{{{r}_{0}}^{2}}}$+v0 |
4.下列说法正确的是( )
| A. | 掷出的铅球速度不大,所以其惯性很小,可以用手去接 | |
| B. | 用力打出的乒乓球速度很大,因此其惯性很大,不能用手去接 | |
| C. | 相同的两辆车,速度大的比速度小的难以停下,是因为速度大的车惯性大 | |
| D. | 相同的两辆车,惯性大小相同 |
 “嫦娥三号”探测器成功实施近月制动,顺利进入环月轨道,并在月球成功地进行了一系列研究.为人类征服太空奠定基础,“嫦娥四号”择日发射,若把探测器环月运行轨道可视为圆轨道,忽略地球及其他天体的引力对探测器的影响,设探测器环月运行轨道半径为r,月球半径为R,运行周期为T,引力常量为G,求:
“嫦娥三号”探测器成功实施近月制动,顺利进入环月轨道,并在月球成功地进行了一系列研究.为人类征服太空奠定基础,“嫦娥四号”择日发射,若把探测器环月运行轨道可视为圆轨道,忽略地球及其他天体的引力对探测器的影响,设探测器环月运行轨道半径为r,月球半径为R,运行周期为T,引力常量为G,求: