题目内容
18.建筑工程中的“打桩”是利用重锤的冲击克服泥土对桩柱的阻力,使桩柱插入泥土到达预定深度的过程.如图甲所示,设打桩机重锤的质量为m,桩柱的质量为M.打桩过程可简化如下:开始时,桩柱下端在地表面没有进入泥土,提升重锤到距离桩柱上端h高度后使其自由落下,重锤撞击桩柱上端,经极短时间的撞击使两者以共同的速度一起向下移动一段距离后停止.然后再次提升重锤,重复打桩过程,逐渐把桩柱打到预定深度.设桩柱向下移动的过程中泥土对桩柱的阻力f的大小与桩柱打入泥土中的深度x成正比,其函数表达式f=kx(k为大于0的已知常量),f-x图象如图乙所示.已知重力加速度大小为g.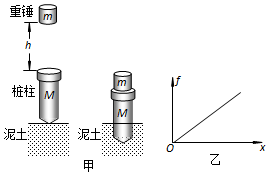
(1)求重锤与桩柱第一次碰撞过程中损失的机械能;
(2)在解决一些实际问题时,有时为了简化问题,需要忽略一些数值相对较小的量,这对最终的计算结果并没有太大的影响.如在(1)问中,我们忽略了重锤所受重力,可用竖直方向动量守恒定律处理问题.同样,在分析桩柱进入泥土的过程中,有时也可以忽略重锤和桩柱所受的重力.请你说明在重锤撞击桩柱效果相同的条件下,由于忽略重锤和桩柱所受的重力带来计算结果的差异,对重锤撞击桩柱后一起进入泥土中的深度的计算结果差异的影响.
(3)如果不计桩柱下移过程重锤和桩柱所受重力的影响,设每次提升重锤距桩帽的高度均为h,求经过三次撞击后铁桩被打入泥土的深度.
分析 (1)先自由落体运动的规律求出重锤与桩柱第一次碰撞前瞬间的速度,由动量守恒定律求出碰后共同速度,从而求得碰撞过程中损失的机械能.
(2)分析重力的影响,明确在打击中由于高度下降,重力做功,因此使计算变的复杂;
(3)不计重力影响,则根据功能关系可知,每次打击后的动能全部克服阻力做功,根据图象可求出克服阻力所做的功.
解答 解:(1)碰撞前瞬间重锤速度:$v=\sqrt{2gh}$
取竖直向下方向为正方向,由竖直方向动量守恒有:
mv=(M+m)v共
即 $m\sqrt{2gh}=(M+m){v_共}$
得:${v_共}=\frac{{m\sqrt{2gh}}}{(M+m)}$
因此损失的机械能:$△E=\frac{1}{2}m{v^2}-\frac{1}{2}(M+m)v_共^2=\frac{1}{2}m•2gh-\frac{1}{2}\frac{{{m^2}•2gh}}{(M+m)}=\frac{Mmgh}{(M+m)}$
(2)每次重锤的撞击会产生相同的初动能,若忽略重锤和桩柱的重力,则相同的初动能使得每次克服阻力做功也相同;若没有忽略重锤和桩柱的重力,则由于每次撞击桩柱下降的深度不同,阻力做功也不同,计算会更加复杂.
(3)由于每次提升重锤距桩帽的高度均为h,每次碰撞后瞬间的速度均为v共,
设三次打击后共下降x,则由图象可知,克服阻力做功W=$\frac{1}{2}$kx2
由能量守恒定律得:
$3×\frac{1}{2}(M+m)v_共^2=\frac{1}{2}k{x^2}$
解得,经过三次撞击后被打入泥土的深度:$x=\sqrt{\frac{{6{m^2}gh}}{(M+m)k}}$.
答:
(1)重锤与桩柱第一次碰撞过程中损失的机械能是$\frac{Mmgh}{M+m}$.
(2)没有忽略重锤和桩柱的重力,则由于每次撞击桩柱下降的深度不同,阻力做功也不同,计算会更加复杂.
(3)经过三次撞击后铁桩被打入泥土的深度为$\sqrt{\frac{{6{m^2}gh}}{k(M+m)}}$
点评 本题综合考查动量守恒定律、功能关系等内容,要注意正确分析题意,并且根据题意构建物理模型,从而根据所学过的物理知识进行分析,找出合适的物理规律求解即可,本题对学生的分析能力要求较高,应在平时学习中注意练习.

 物体第1s内由静止向右做加速度为1m/s2的匀加速运动,第2s内加速度方向向左,大小不变.以后每隔1s加速度的方向都改变一次,但大小不变,其速度图象如图所示,则100s后物体在( )
物体第1s内由静止向右做加速度为1m/s2的匀加速运动,第2s内加速度方向向左,大小不变.以后每隔1s加速度的方向都改变一次,但大小不变,其速度图象如图所示,则100s后物体在( )| A. | 原位置 | B. | 原位置右50m | C. | 原位置左50m | D. | 原位置右0.5m |
 如图所示,质量m=1kg小物块(可视为质点),在沿半径方向的轻弹簧作用下在凹形槽上处于静止状态,弹簧的一端固定在圆心θ处,弹簧与竖直方向的夹角θ=37°.物块与凹形槽间的动摩擦因数为0.75,g=10m/s2,sin 37°=0.6,cos 37°=0.8,则( )
如图所示,质量m=1kg小物块(可视为质点),在沿半径方向的轻弹簧作用下在凹形槽上处于静止状态,弹簧的一端固定在圆心θ处,弹簧与竖直方向的夹角θ=37°.物块与凹形槽间的动摩擦因数为0.75,g=10m/s2,sin 37°=0.6,cos 37°=0.8,则( )| A. | 弹簧一定处于压缩状态 | B. | 弹簧可能处于伸长状态 | ||
| C. | 槽对物块的摩擦力大小一定是6N | D. | 物块对槽的压力大小一定是8N |
| A. | 在地球上的同一地点,一切物体在自由落体运动中的加速度大小都相同 | |
| B. | 在地球上的同一地点,重力加速度的方向都相同 | |
| C. | 在地球上纬度不同的地方,重力加速度的大小不同 | |
| D. | 地球赤道处的重力加速度比两极的重力加速度大 |
| A. | 加速度为8m/s2 | |
| B. | 2s内受到的冲量为32N•s | |
| C. | 在相同的时间内,动量的增量一定相等 | |
| D. | 通过相同的距离,动量的增量也可能相等 |
 如图所示电路中,R1=R2=R3=2Ω,R4=1Ω,若A、B两端的电压为10V,则通过电阻R1、R2、R3、R4的电流分别为5A、2.5A、2.5A、5A.
如图所示电路中,R1=R2=R3=2Ω,R4=1Ω,若A、B两端的电压为10V,则通过电阻R1、R2、R3、R4的电流分别为5A、2.5A、2.5A、5A.
 如图所示,空间中存在着水平向右的匀强电场,一长为1m的细线上端固定于O点,下端拴一质量为m=$\sqrt{3}$kg、带电荷量q=1C的小球.现将细线拉直且水平,由球静止释放小球,当细线转过60°时,小球到达B点速度恰好为零,重力加速度g=10m/s2.求:
如图所示,空间中存在着水平向右的匀强电场,一长为1m的细线上端固定于O点,下端拴一质量为m=$\sqrt{3}$kg、带电荷量q=1C的小球.现将细线拉直且水平,由球静止释放小球,当细线转过60°时,小球到达B点速度恰好为零,重力加速度g=10m/s2.求: