题目内容
20．
如图所示，光滑斜面的倾角θ=30°，一小球从斜面底端O点正上方，距O点高度h=5m处由静止下落，小滑块从斜面上的P点由静止沿斜面下滑，若小球和滑块同时开始运动并在O点相遇，不计空气阻力，求：O、P两点之间的距离．（g=10m/s2）
分析 设滑块的加速度大小为a，小球和滑块的运动时间为t，小球做自由落体运动，可由自由落体运动的规律求出时间．滑块做匀加速运动，由牛顿第二定律和位移公式结合求解L．
解答 解：设滑块的加速度大小为a，小球和滑块的运动时间为t
小球做自由落体运动，由自由落体运动的规律有：$h=\frac{1}{2}g{t}^{2}$ ①
代入数据解得：t=1s
对滑块，由牛顿第二定律有
mgsinθ=ma ②
对滑块，由匀变速运动的规律有：L=$\frac{1}{2}a{t}^{2}$③
由①～③式并代入数据可得：L=2.5m
答：OP之间的距离L是2.5m．
点评 本题关键抓住两个运动的同时性，运用运动学公式和牛顿第二定律进行求解．
练习册系列答案
相关题目
10．两点电荷形成电场的电场线分布如图所示，A、B是电场线上的两点，下列判断正确的是（ ）
| A． | A、B两点的电场强度大小不等，方向相同 | |
| B． | A、B两点的电场强度大小相等，方向不同 | |
| C． | 左边电荷带负电，右边电荷带正电 | |
| D． | 两电荷所带电荷量相等 |
11．如图所示，用细绳把小球悬挂起来，当小球静止时，下列说法中正确的是（ ）
| A． | 小球对细绳的拉力和细绳对小球的拉力是一对作用力和反作用力 | |
| B． | 小球受到的重力和小球对细绳的拉力是一对作用力和反作用力 | |
| C． | 小球受到的重力和细绳对小球的拉力是一对平衡力 | |
| D． | 小球受到的重力和小球对细绳的拉力是一对平衡力 |
8．
如图所示，电动机线圈电阻为R，电动机正常工作时，两端的电压为U，通过的电流为I，电源电动势为E，内阻为r，下列说法中正确的是（ ）
如图所示，电动机线圈电阻为R，电动机正常工作时，两端的电压为U，通过的电流为I，电源电动势为E，内阻为r，下列说法中正确的是（ ）| A． | 电源的总功率为UI | B． | 电动机的输入总功率为UI | ||
| C． | 电动机输出的机械功率为UI-I2R | D． | 电动机线圈产生的热功率为$\frac{{U}^{2}}{R}$ |
15．物体甲的x-t图象和物体乙的v-t图象分别如图所示，则这两物体的运动情况是（ ）
| A． | 甲在整个t=6s时间内运动方向一直不变，它通过的总位移大小为6m | |
| B． | 甲在整个t=6s时间内有来回运动，它通过的总位移为零 | |
| C． | 乙在整个t=6s时间内有来回运动，它通过的总位移为零 | |
| D． | 乙在整个t=6s时间内运动方向一直不变，它通过的总位移大小为4m |
5．
如图所示的电路中，电源内阻不可忽略，若调整可变电阻R的阻值，可使电压表
的示数减小△U（电压表为理想电表），在这个过程中（ ）
如图所示的电路中，电源内阻不可忽略，若调整可变电阻R的阻值，可使电压表的示数减小△U（电压表为理想电表），在这个过程中（ ）| A． | R2两端的电压增加，增加量一定等于△U | |
| B． | 流过R的电流会减小 | |
| C． | 路端电压减小，减少量一定等于△U | |
| D． | △U和干路电流的变化△I的比值保持不变 |
12．
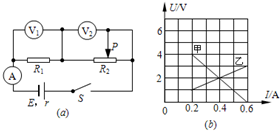在如图（a）所示的电路中，R1为定值电阻，R2为滑动变阻器．闭合开关S，将滑动变阻器的滑动触头P从最右端滑到最左端，两个电压表（内阻极大）的示数随电路中电流变化的完整过程图线如图（b）所示．则下列说法正确的是（ ）
在如图（a）所示的电路中，R1为定值电阻，R2为滑动变阻器．闭合开关S，将滑动变阻器的滑动触头P从最右端滑到最左端，两个电压表（内阻极大）的示数随电路中电流变化的完整过程图线如图（b）所示．则下列说法正确的是（ ）| A． | 图线甲是电压表V1示数随电流变化的图线 | |
| B． | 电源内电阻的阻值为5Ω | |
| C． | 电源的最大输出功率为1.5W | |
| D． | 滑动变阻器R2的最大功率为0.9W | |
| E． | 电源电动势为6V |
如图所示，装置可绕竖直轴O′O转动，可视为质点的小球A与两细线连接后分别系