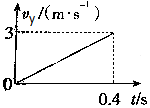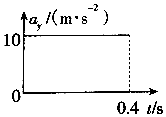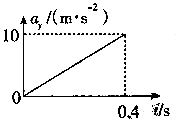题目内容
20.如图甲所示,2013年北京时间12月6日17时47分,“嫦娥三号”经过地月转移轨道后,经过两次近月制动,进入距离月球表面高度为100km的环月圆轨道运动,经过第三次近月制动后进入椭圆轨道,并于12月10日到达离月球表面高度为15km的虹湾区上空,着陆器准备软着陆,已知月球的半径为1740km,月球表面的重力加速度为1.6m/s2.(1)求“嫦娥三号”在环月圆轨道与椭圆轨道交汇点的加速度和着陆器在椭圆轨道近月点的加速度的比值.
(2)如图乙所示,如果我们把“嫦娥三号”的着陆器在虹湾区上空100m之后的软着陆过程简化为运动轨迹A→B→C,AB直线段与竖直方向的夹角为60°,AB阶段的制动力恒定且与运动轨迹垂直,着陆器在A点处的速度可视为零,在B点处关闭发动机,则着陆器在该软着陆过程所用的总时间为多少?着陆前瞬间的速度大小为多少?

分析 (1)根据牛顿第二定律求出“嫦娥三号”在环月圆轨道与椭圆轨道交汇点的加速度和着陆器在椭圆轨道近月点的加速度,再求比值;
(2)根据牛顿第二定律和运动学公式求出A→B的时间,以及B点的速度.再由运动学公式求出B→C的时间,即可求出软着陆的总时间;根据动能定理即可求出着陆前瞬间的速度大小.
解答 解:(1)环月圆轨道半径${R}_{1}^{\;}=1740km+100km=1840km$,椭圆轨道的近月点到月心的距离为${R}_{2}^{\;}=1740km+15km=1755km$
则“嫦娥三号”在环月圆轨道与椭圆轨道交汇点时由牛顿第二定律有:${F}_{1}^{\;}=G\frac{mM}{{R}_{1}^{2}}=m{a}_{1}^{\;}$
着陆器在椭圆轨道近月点时由牛顿第二定律有:${F}_{2}^{\;}=G\frac{mM}{{R}_{2}^{2}}=m{a}_{2}^{\;}$
故有$\frac{{a}_{1}^{\;}}{{a}_{2}^{\;}}=\frac{{R}_{2}^{2}}{{R}_{1}^{2}}=\frac{175{5}_{\;}^{2}}{184{0}_{\;}^{2}}=0.91$
(2)A→B过程中$a=\frac{{F}_{合}^{\;}}{m}={g}_{月}^{\;}cos60°=0.8m/{s}_{\;}^{2}$
着陆器到达B点的时间为${t}_{1}^{\;}$,有$192m=\frac{1}{2}a{t}_{1}^{2}$,得${t}_{1}^{\;}=4\sqrt{30}s$
到达B点的速度为${v}_{1}^{\;}=a{t}_{1}^{\;}=\frac{16\sqrt{30}}{5}m/s$
B→C过程中,${v}_{1y}^{\;}={v}_{1}^{\;}cos60°=\frac{8\sqrt{30}}{5}m/s$
着陆前瞬间的竖直速度为${v}_{2y}^{\;}$,则
${v}_{2y}^{2}-{v}_{1y}^{2}=2{g}_{月}^{\;}×4m$,得${v}_{2y}^{\;}=\frac{8\sqrt{35}}{5}m/s$
则从B→C过程的运动时间${t}_{2}^{\;}=\frac{{v}_{2y}^{\;}-{v}_{1y}^{\;}}{{g}_{月}^{\;}}$
着陆器软着陆的总时间为$t={t}_{1}^{\;}+{t}_{2}^{\;}=22.35s$
着陆前由动能定理有$m{g}_{月}^{\;}h=\frac{1}{2}m{v}_{\;}^{2}$
解得$v=8\sqrt{5}m/s$
答:(1)“嫦娥三号”在环月圆轨道与椭圆轨道交汇点的加速度和着陆器在椭圆轨道近月点的加速度的比值0.91.
(2)则着陆器在该软着陆过程所用的总时间为22.35s,着陆前瞬间的速度大小为8$\sqrt{5}$m/s
点评 本题考查天体运动、牛顿第二定律和曲线运动的综合应用,意在考查考生对物理过程的分析综合能力和运算能力,关键是理解题意,物理情境搞清楚,然后选择合适的规律列式.

| A. | 4.5m/s | B. | 5m/s | C. | 6m/s | D. | 7.5m/s |
 如图所示,电源电动势为ε,电源内阻为r,当电键K闭合时,正确的判断是( )
如图所示,电源电动势为ε,电源内阻为r,当电键K闭合时,正确的判断是( )| A. | 电压表的读数变小,电流表的读数变小 | |
| B. | 电压表的读数变小,电流表的读数增大 | |
| C. | 电压表的读数增大,电流表的读数变小 | |
| D. | 电压表的读数增大,电流表的读数增大 |
| A. | 导体中的自由电荷不停地运动 | B. | 导体接在电路上 | ||
| C. | 导体两端存在电流 | D. | 导体两端存在电压 |
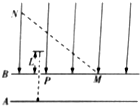 如图所示,平行金属板A、B间存在加速电压,一个不计重力、带正电荷的粒子从A板附近由静止开始被加速,恰好从B板小孔P飞出,B板上方分布有场强为E的匀强电场,当场强方向竖直向下时,粒子从小孔P打入电场,能在电场中上升的最大高度为L.空间中两点M、N连线与B板成45°角.
如图所示,平行金属板A、B间存在加速电压,一个不计重力、带正电荷的粒子从A板附近由静止开始被加速,恰好从B板小孔P飞出,B板上方分布有场强为E的匀强电场,当场强方向竖直向下时,粒子从小孔P打入电场,能在电场中上升的最大高度为L.空间中两点M、N连线与B板成45°角. 如图所示为一由双刀双掷电键S、两节干电池(每节干电池的电动势E=1.5V,内阻r=1Ω)和一个小灯泡(额定电压为2.5V,额定电流为0.15A)组成的电路,那么:
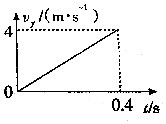
如图所示为一由双刀双掷电键S、两节干电池(每节干电池的电动势E=1.5V,内阻r=1Ω)和一个小灯泡(额定电压为2.5V,额定电流为0.15A)组成的电路,那么: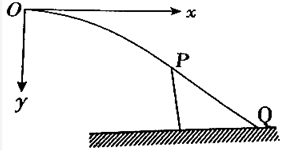 将小球以3m/s的速度水平抛出,它落地速度为5m/s,以vx、vy分别表示水平、竖直分速度,以ay表示竖直分加速度,取g=10m/s2,则图中正确的是( )
将小球以3m/s的速度水平抛出,它落地速度为5m/s,以vx、vy分别表示水平、竖直分速度,以ay表示竖直分加速度,取g=10m/s2,则图中正确的是( )