题目内容
20. 质量均为m的A、B小球套在一竖直光滑圆环上,并由一不可伸长的轻绳相连.现施加一力F作用于A球上使A球处于静止状态,此时A球与圆环恰好无作用力,B球位于与圆心等高处.已知重力加速度为g,则下列说法正确的是( )
质量均为m的A、B小球套在一竖直光滑圆环上,并由一不可伸长的轻绳相连.现施加一力F作用于A球上使A球处于静止状态,此时A球与圆环恰好无作用力,B球位于与圆心等高处.已知重力加速度为g,则下列说法正确的是( )| A. | 力F大小为$\sqrt{5}$mg | |
| B. | B球所受的圆环给的弹力与绳子拉力大小之比为$\sqrt{2}$:1 | |
| C. | 去掉力F瞬间,绳子拉力大小为$\frac{\sqrt{2}}{2}$mg | |
| D. | 去掉力F前后,B球所受圆环给的弹力大小不变 |
分析 施加F时,AB都处于静止状态,分别对AB小球受力分析,根据平衡条件以及力的分解与合成原则求出F的大小以及B球所受的圆环给的弹力与绳子拉力大小关系,去掉力F瞬间,由于绳不可伸长,两球速度为零,所以向心加速度为零,但两球有相同的切向加速度,根据牛顿第二定律列式求解绳子拉力,根据B球指向圆心的合力为零,求出圆环对B的弹力即可.
解答 解:A、B处于静止状态,对B受力分析,受到重力、绳子拉力以及圆环对B水平向左的弹力,根据平衡条件得:
绳子拉力T=$\frac{mg}{cos45°}=\sqrt{2}mg$,弹力N1=mgtan45°=mg,则B球所受的圆环给的弹力与绳子拉力大小之比为1:$\sqrt{2}$,
对A受力分析,A受到重力、绳子拉力以及F作用,处于平衡状态,则F的大小等于mg和绳子拉力的合力,根据力的分解与合成原则得:F=$\sqrt{(mg+Tsin45°)^{2}+(Tcos45°)^{2}}=\sqrt{5}mg$,故A正确,B错误;
C、去掉力F瞬间,由于绳不可伸长,则两球速度为零,所以向心加速度为零,但两球有相同的切向加速度,则根据牛顿第二定律可知:
A小球:T′cos45°=ma
B小球:mg-Tcos45°=ma
解得$a=\frac{g}{2}$,$T′=\frac{\sqrt{2}}{2}mg$,故C正确;
D、去掉力F后,B球指向圆心的合力为零,则圆环对B的弹力大小$N′=T′cos45°=\frac{1}{2}mg$,则去掉力F前后,B球所受圆环给的弹力大小发生变化,故D错误.
故选:AC
点评 本题注意考查了共点力平衡条件以及牛顿第二定律的直接应用,要求同学们能正确分析物体的受力情况,明确撤去F后与撤去F前的不同点,难度适中.

练习册系列答案
相关题目
10.如图所示,一水平力F作用在物体B上,A、B一起做匀速直线运动,则( )


| A. | A、B之间无摩擦力 | B. | A受到的摩擦力水平向右 | ||
| C. | B与地面之间无摩擦力 | D. | 地面对B的摩擦力水平向右 |
8.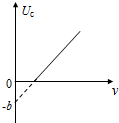 在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
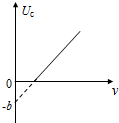 在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )
在某次光电效应实验中,得到的遏止电压Uc与入射光的频率v的关系如图所示,若该直线的斜率和纵截距分别为k和-b,电子电荷量的绝对值为e,则( )| A. | 普朗克常量可表示为$\frac{k}{e}$ | |
| B. | 若更换材料再实验,得到的图线的k不改变,b改变 | |
| C. | 所用材料的逸出功可表示为eb | |
| D. | b由入射光决定,与所用材料无关 |
15.有关近代物理知识,下列叙述中正确的是( )
| A. | 康普顿效应深入地揭示了光的粒子性的一面,该效应表明光子除了具有能量之外还具有动量 | |
| B. | 碘-131的半衰期大约为8天,40天后,碘-131就只剩下原来的$\frac{1}{32}$ | |
| C. | Th核发生一次α衰变后,新核与原来的原子核相比,中子数减少了4 | |
| D. | 比结合能越大,原子核中核子结合得越不牢固,原子核越不稳定 | |
| E. | 处于基态的氢原子吸收一个光子后跃迁到激发态,再向低能级跃迁时辐射出的光子的频率一定不大于入射光子的频率 |
5.地球同步卫星的运行速率为v1,向心加速度为a1,角速度为ω1,周期为T1;地球赤道上物体随地球自转的速率为v2,向心加速度为a2,角速度为ω2,周期为T2;地球近地卫星的速率为v3,向心加速度为a3,角速度为ω3,周期为T3.则( )
| A. | v3>v1>v2 | B. | a3=a2>a1 | C. | ω3>ω1=ω2 | D. | T3>T1>T2 |
12.发现万有引力定律的物理学家是( )
| A. | 安培 | B. | 爱因斯坦 | C. | 牛顿 | D. | 卡文迪许 |
10. 在匀强电场中有一个半径为R=1m的圆,电场方向与圆所在平面平行,O,P两点电势差为10V,一个电子在该匀强电场中仅受电场力作用下运动,且在P,Q两点上速度方向与圆的切线一致,速度大小相同,则( )
在匀强电场中有一个半径为R=1m的圆,电场方向与圆所在平面平行,O,P两点电势差为10V,一个电子在该匀强电场中仅受电场力作用下运动,且在P,Q两点上速度方向与圆的切线一致,速度大小相同,则( )
 在匀强电场中有一个半径为R=1m的圆,电场方向与圆所在平面平行,O,P两点电势差为10V,一个电子在该匀强电场中仅受电场力作用下运动,且在P,Q两点上速度方向与圆的切线一致,速度大小相同,则( )
在匀强电场中有一个半径为R=1m的圆,电场方向与圆所在平面平行,O,P两点电势差为10V,一个电子在该匀强电场中仅受电场力作用下运动,且在P,Q两点上速度方向与圆的切线一致,速度大小相同,则( )| A. | 电子从P到Q的运动过程中,电势能先增大后减小 | |
| B. | 电子可能做匀速圆周运动 | |
| C. | 该匀强电场的电场强度E=10V/m | |
| D. | 圆周上两点间电势差的最大值为20$\sqrt{2}$V |
 发卡弯是形容赛道上某个弯角程度的词,比较形象.发卡弯一般的角度都接近180°.赛车过这种弯道的时候,最理想的过弯路径是“外圈人弯,贴弯心出弯”.如图所示为赛车场的一个水平发卡弯,转弯处为圆心在O点的半圆,内外半径分别为r和2r,r=10m.一辆质量为m=800kg的赛车(含车手的质量)从A处进弯,从A′点出弯,过弯路线是以O′为圆心的半圆,OO′=r.赛车以不打滑的最大速率v=72km/h通过弯道(赛车速率不变),赛车能以此车速过弯是因为赛车形状都设计得使其上下方空气有一压力差-气动压力,从而增大了对地面的正压力.已知赛车轮胎与赛道附着系数η=0.8,附着系数可以看成是轮胎与路面的摩擦系数.这个系数越大,可利用的附着力(可视为静摩擦力)就越大,汽车就越不容易打滑,轮胎与赛道路面的滑动摩擦力与最大静摩擦力相等.求赛车沿此线路过弯时气动压力的最小值?
发卡弯是形容赛道上某个弯角程度的词,比较形象.发卡弯一般的角度都接近180°.赛车过这种弯道的时候,最理想的过弯路径是“外圈人弯,贴弯心出弯”.如图所示为赛车场的一个水平发卡弯,转弯处为圆心在O点的半圆,内外半径分别为r和2r,r=10m.一辆质量为m=800kg的赛车(含车手的质量)从A处进弯,从A′点出弯,过弯路线是以O′为圆心的半圆,OO′=r.赛车以不打滑的最大速率v=72km/h通过弯道(赛车速率不变),赛车能以此车速过弯是因为赛车形状都设计得使其上下方空气有一压力差-气动压力,从而增大了对地面的正压力.已知赛车轮胎与赛道附着系数η=0.8,附着系数可以看成是轮胎与路面的摩擦系数.这个系数越大,可利用的附着力(可视为静摩擦力)就越大,汽车就越不容易打滑,轮胎与赛道路面的滑动摩擦力与最大静摩擦力相等.求赛车沿此线路过弯时气动压力的最小值?