题目内容
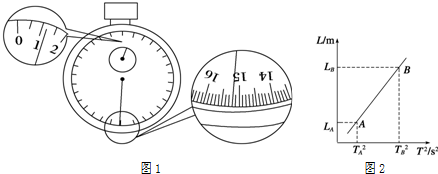
11.做“用单摆测定重力加速度”的实验,(1)为测量单摆的摆动周期,测量时间应从摆球经过平衡位置时开始计时;某次测定了40次全振动的时间如图1中秒表所示,那么秒表读数是75.2s.
(2)改变摆长l,共测定了6组摆长l和对应的周期T.为了求出当地的重力加速度g,3位同学提出了3种不同的处理方法:
A.从测定的6组对应值中任意选取1组,用公式g=$\frac{4{π}^{2}l}{{T}^{2}}$求出g作为测量值
B.先分别求出6个l值的平均值$\overline{l}$和6个T值的平均值$\overline{T}$,再用公式g=$\frac{4{π}^{2}\overline{i}}{\overline{T}}$求出g作为测量值
C.先用6组l和T的值,用公式g=$\frac{4{π}^{2}l}{{T}^{2}}$求出6个对应的g值,再求这6个值的平均值作为测量值
以上3种方法中,错误的是B,其余正确方法中,偶然误差最大的是A(填入相应的字母).
(3)某同学只测量了悬点到球间摆线的长度L,测得多组L和对应的周期T,画出如图2所示的L-T 2图线,并在图线上选取了A、B两个点,其坐标如图所示.据此可得计算重力加速度的表达式为g=$\frac{4{π}^{2}({L}_{B}-{L}_{A})}{{{T}_{B}}^{2}-{{T}_{A}}^{2}}$.该同学测摆长时漏加了小球半径,而其它测量、计算均无误,则用上述方法算得的g值和真实值相比是不变的(选填“偏大”、“偏小”或“不变”).
分析 (1)秒表的读数等于小盘读数加上大盘读数;
(2)根据L与T是非线性关系,分析实验错误的方法.采用一组数据计算偶然误差较大.
(3)根据单摆的周期公式,得出L-T2的关系式,结合图线的斜率求出重力加速度的表达式.
解答 解:(1)秒表的小盘读数为60s,大盘读数为15.2s,则最终读数为75.2s.
(2)分别求出6个l值的平均值$\overline{l}$和6个T值的平均值$\overline{T}$,表达式g=$\frac{4{π}^{2}l}{{T}^{2}}$就不成立了,故B错误;
根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$,从测定的6组对应值中任意选取1组,偶然误差最大,所以偶然误差最大的选A.
(3)根据T=2π$\sqrt{\frac{L}{g}}$得,L=$\frac{g{T}^{2}}{4{π}^{2}}$,则图线的斜率k=$\frac{{L}_{B}-{L}_{A}}{{T}_{B}^{2}-{T}_{A}^{2}}$=$\frac{g}{4{π}^{2}}$,解得:g=$\frac{4{π}^{2}({L}_{B}-{L}_{A})}{{T}_{B}^{2}-{T}_{A}^{2}}$.
通过g的表达式可以知道,漏加了小球半径后,(LB-LA)不变,故不影响最后结果.
故答案为:(1)75.2;(2)B;A;(3)$\frac{4{π}^{2}({L}_{B}-{L}_{A})}{{T}_{B}^{2}-{T}_{A}^{2}}$;不变.
点评 本题考查了秒表读数、实验数据处理等问题;本题的解题关键明确实验原理、误差来源,知道偶然误差的特点和减小方法,会用图象法分析数据.

| A. | 在力学的分析计算中,只能采用国际制单位,不能采用其他单位 | |
| B. | 力学单位制中,选为基本单位的物理量有力、时间、质量 | |
| C. | 力学单位制中,采用国际单位制的基本单位有千克、厘米、秒 | |
| D. | 单位制中的导出单位可以用基本单位来表示 |
 如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )
如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以一定的初速度v向平台边缘滑去,着地时的速度方向与水平地面的夹角为45°(取重力加速度g=10m/s2).由此可知下列各项中错误的是( )| A. | 滑雪者离开平台边缘时的速度大小是5.0 m/s | |
| B. | 滑雪者着地点到平台边缘的水平距离是2.5 m | |
| C. | 滑雪者在空中运动的时间为0.5 s | |
| D. | 着地时滑雪者重力做功的瞬时功率是200 W |
 在如图所示的电路中,电源两端的电压恒定,D为发光二极管(电流越大,发出的光越强),R0为定值电阻,R为光敏电阻(D发出的光越强,R的阻值越小),下列说法正确的是( )
在如图所示的电路中,电源两端的电压恒定,D为发光二极管(电流越大,发出的光越强),R0为定值电阻,R为光敏电阻(D发出的光越强,R的阻值越小),下列说法正确的是( )| A. | 当滑动触头P向左移动时,R0消耗的功率增大 | |
| B. | 当滑动触头P向左移动时,R0消耗的功率减少 | |
| C. | 当滑动触头P向左移动时,R0消耗的功率可能不变 | |
| D. | 无论怎样移动滑动触头P,R0消耗的功率都不变 |
| A. | 计算高铁通过某一山洞时间时,可将高铁看成质点 | |
| B. | 高铁速度显示屏上显示的是瞬时速率 | |
| C. | 题中所给的高铁设计时速350公里是指平均速度 | |
| D. | 题中所给的“184.7 km”指的是位移大小 |

| A. | 第 1s内和第 3s 内的运动方向相反 | |
| B. | 第 3s内和第 4s 内的加速度相同 | |
| C. | 第 1s内和第 4s 内的位移大小不相等 | |
| D. | 0~2s 和 0~4s 内的平均速度大小相等 |
 如图,质量m0=1kg的平板B上表面水平,板长L=1m,开始时静止在光滑水平面上,在平板左端静止着一块质量mA=1kg的物块A,一颗质量mB=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后,速度变为v=200m/s,已知A与B之间的动摩擦因数μ=0.2,求:
如图,质量m0=1kg的平板B上表面水平,板长L=1m,开始时静止在光滑水平面上,在平板左端静止着一块质量mA=1kg的物块A,一颗质量mB=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后,速度变为v=200m/s,已知A与B之间的动摩擦因数μ=0.2,求: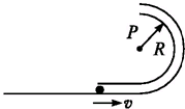 如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求:
如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求: