题目内容
17. 如图所示,平行导轨倾斜放置,倾角θ=37°,匀强磁场的方向垂直于导轨平面向上,磁感应强度B=4T,质量为m=2kg的金属棒ab垂直放在导轨上,ab与导轨平面间的动摩擦因数μ=0.25.ab的电阻r=1Ω,平行导轨间的距离L=1m,R1=R2=18Ω,导轨电阻不计,ab由静止开始下滑运动x=3.5m后达到匀速.sin37°=0.6,cos37°=0.8.求:
如图所示,平行导轨倾斜放置,倾角θ=37°,匀强磁场的方向垂直于导轨平面向上,磁感应强度B=4T,质量为m=2kg的金属棒ab垂直放在导轨上,ab与导轨平面间的动摩擦因数μ=0.25.ab的电阻r=1Ω,平行导轨间的距离L=1m,R1=R2=18Ω,导轨电阻不计,ab由静止开始下滑运动x=3.5m后达到匀速.sin37°=0.6,cos37°=0.8.求:(1)ab在导轨上匀速下滑的速度多大?
(2)ab匀速下滑时ab两端的电压为多少?
(3)ab由静止到匀速过程中电阻R1产生的焦耳热Q1为多少?
分析 (1)ab在导轨上匀速下滑时ab棒受力平衡,推导出安培力与速度的关系,由平衡条件即可求得速度.
(2)由公式E=Blv求出匀速时ab产生的感应电动势,再由欧姆定律求解ab两端的电压.
(3)根据能量守恒定律或动能定理求解电阻R1产生的焦耳热Q1.
解答 解:(1)ab棒匀速下滑时,有 mgsin37°=μmgcos37°+FB
又 FB=BIL
I=$\frac{E}{R+r}$
E=BLv
则得 FB=$\frac{{B}^{2}{L}^{2}v}{R+r}$
式中 R=$\frac{1}{2}{R}_{1}$=9Ω
解得v=$\frac{mg(sin37°-μcos37°)(R+r)}{{B}^{2}{L}^{2}}$=$\frac{2×10×(sin37°-0.25×cos37°)×(9+1)}{{4}^{2}×{1}^{2}}$=5m/s
(2)由E=Blv,解得E=4×1×5V=20V
由I=$\frac{E}{R+r}$,解得I=$\frac{20}{10}$A=2A
由U=E-Ir,解得ab两端的电压为U=18V
(3)根据动能定理得:mgsin37°x-μmgcos37°x+W安=$\frac{1}{2}m{v}^{2}$
又W安=-Q
代入解得Q=3J
则电阻R1产生的焦耳热Q1=$\frac{1}{2}$×$\frac{R}{R+r}$Q=$\frac{1}{2}×\frac{9}{9+1}$×3J=1.35J
答:
(1)ab在导轨上匀速下滑的速度是5m/s.
(2)ab匀速下滑时ab两端的电压为18V.
(3)ab由静止到匀速过程中电阻R1产生的焦耳热Q1为1.35J.
点评 电磁感应中导体切割引起的感应电动势在考试中涉及较多,应明确受力分析、功能关系等的灵活应用,注意平衡状态的处理.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 周期 | B. | 质量 | C. | 向心力 | D. | 离地心的距离 |
 如图所示,条形磁铁放在水平桌面上,在其正中央的右上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向外的电流,则( )
如图所示,条形磁铁放在水平桌面上,在其正中央的右上方固定一根长直导线,导线与磁铁垂直,给导线通以垂直纸面向外的电流,则( )| A. | 磁铁对桌面压力减小,磁铁受到桌面向左摩擦力作用 | |
| B. | 磁铁对桌面压力减小,磁铁受到桌面向右摩擦力作用 | |
| C. | 磁铁对桌面压力增大,磁铁不受桌面的摩擦力作用 | |
| D. | 磁铁对桌面压力增大,磁铁受到桌面的摩擦力作用 |
| A. | 加速度与速度方向一定相同 | B. | 加速度一定增大 | ||
| C. | 位移一定增大 | D. | 加速度方向可能与速度方向相反 |
 封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度T关系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.
封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度T关系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA.



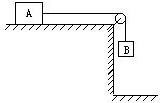 如图所示,mA=4kg,mB=1kg,A与桌面间的动摩擦因数μ=0.2,B与地面间的距离s=0.8m,A、B间绳子足够长,A、B原来静止,求:
如图所示,mA=4kg,mB=1kg,A与桌面间的动摩擦因数μ=0.2,B与地面间的距离s=0.8m,A、B间绳子足够长,A、B原来静止,求: 一个气球以10m/s的速度匀速竖直上升,气球下面系着一个重物,当气球上升到下面的重物离地面120m时,系重物的绳断了,问这时起,重物经过多长时间落到地面?重物着地时速度多大?(g取10m/s2)
一个气球以10m/s的速度匀速竖直上升,气球下面系着一个重物,当气球上升到下面的重物离地面120m时,系重物的绳断了,问这时起,重物经过多长时间落到地面?重物着地时速度多大?(g取10m/s2)