题目内容
4. 如图所示为简谐运动的图象.
如图所示为简谐运动的图象.(1)求出它的振幅、周期、初相;
(2)写出它的振动方程.
分析 (1)首先知道振幅是质点离开平衡位置的最大距离,由图象能直接读出;周期是质点完成一次周期性变化所用的时间,也可直接读出;结合振动方程与开始时的位置即可求出初相;
(2)根据周期求出圆频率,代入振幅和初相的数值即可写出振动方程.
解答 解:(1)据图象可知,振幅:A=4cm,周期:T=0.33s-(-0.03)s=0.36s;
根据振动方程:x=Asin(ωt+φ0)
由于t=0时刻质点的位移正在增大,而且大小为2cm,则:2=4sinφ0
所以该简谐振动的初相:φ0=$\frac{π}{6}$
(2)该简谐振动的圆频率:$ω=\frac{2π}{T}=\frac{2π}{0.36}=\frac{50π}{9}$
该简谐振动的振动方程为:x=4sin($\frac{50πt}{9}+\frac{π}{6}$)cm
答:(1)它的振幅是4cm,周期是0.36s,初相是$\frac{π}{6}$;
(2)它的振动方程为x=4sin($\frac{50πt}{9}+\frac{π}{6}$)cm.
点评 由振动图象要能直接质点的振幅、周期,还可读出质点的速度、加速度方向等等,题目较简单.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14.关于天然放射现象,叙述不正确的是( )
| A. | 若使放射性物质与其他物质发生化学反应,其半衰期不会改变 | |
| B. | β衰变所释放的电子不可能是原子核外的电子电离形成的 | |
| C. | 在α、β、γ这三种射线中,γ射线的穿透能力最强,α射线的电离能力最强 | |
| D. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过8次α衰变和10次β衰变 |
15.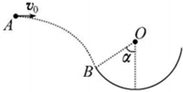 如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )
如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )
 如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )
如图所示,B为半径为R的竖直光滑圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α.一个质量为m的小球在圆轨道左侧的A点以水平速度v0被抛出,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,下列说法正确的是( )| A. | 小球从A运动到B的时间t=$\frac{{v}_{0}}{g}$tanα | |
| B. | A.B之间的距离L=$\frac{{v}_{0}^{2}}{g}$tanα(1+$\frac{tanα}{2}$) | |
| C. | 小球运动到B点时,重力的瞬时功率P=mgv0tanα | |
| D. | 小球运动到竖直圆轨道的最低点时,圆轨道对它的支持力F=$\frac{m{v}_{0}^{2}}{Rco{s}^{2}α}$+3mg-2mgcosα |
12.简谐运动属于下列哪种运动( )
| A. | 匀速运动 | B. | 匀变速运动 | C. | 非匀变速运动 | D. | 无规律运动 |
19.我国“神舟”系列飞船均由长征运载火箭发射,请回答火箭发射和神舟飞船回收的有关问题,下面说法正确的是( )
| A. | 火箭加速发射升空阶段,飞船内座椅对人的支持力大于人对座椅的压力 | |
| B. | 火箭加速发射升空阶段,飞船内人对座椅的作用力大于人的重力 | |
| C. | 神舟飞船减速下降阶段,人对座椅的压力小于人的重力 | |
| D. | 神舟飞船减速下降阶段,人对座椅的压力等于座椅对人的支持力 |
9. 如图为某中国运动员在短道速滑比赛中勇夺金牌的精彩瞬间.假定此时他正沿圆弧形弯道匀速率滑行,则他( )
如图为某中国运动员在短道速滑比赛中勇夺金牌的精彩瞬间.假定此时他正沿圆弧形弯道匀速率滑行,则他( )
 如图为某中国运动员在短道速滑比赛中勇夺金牌的精彩瞬间.假定此时他正沿圆弧形弯道匀速率滑行,则他( )
如图为某中国运动员在短道速滑比赛中勇夺金牌的精彩瞬间.假定此时他正沿圆弧形弯道匀速率滑行,则他( )| A. | 所受的合力为零,做匀速运动 | |
| B. | 所受的合力恒定,做变加速运动 | |
| C. | 所受的合力大小恒定,做匀加速运动 | |
| D. | 所受的合力方向时刻变化,做变加速运动 |
16. 已知氢原子的能级如图所示,现用光子能量介于10~12.9eV范围内的光去照射一群处于基态的氢原子,则下列说法中正确的是( )
已知氢原子的能级如图所示,现用光子能量介于10~12.9eV范围内的光去照射一群处于基态的氢原子,则下列说法中正确的是( )
 已知氢原子的能级如图所示,现用光子能量介于10~12.9eV范围内的光去照射一群处于基态的氢原子,则下列说法中正确的是( )
已知氢原子的能级如图所示,现用光子能量介于10~12.9eV范围内的光去照射一群处于基态的氢原子,则下列说法中正确的是( )| A. | 在照射光中可能被吸收的光子能量有无数种 | |
| B. | 在照射光中可能被吸收的光子能量只有3种 | |
| C. | 照射后可能观测到氢原子发射不同波长的光有10种 | |
| D. | 照射后可能观测到氢原子发射不同波长的光有3种 |
12.关于功和能,下列说法中正确的是( )
| A. | 动能的大小是$\frac{1}{2}$mv2 | |
| B. | 功是矢量,功的方向可能与速度方向相同 | |
| C. | 物体克服重力做的功等于物体重力势能的增量 | |
| D. | 合外力做功为零,那么系统的机械能守恒 |
 如图所示,质量m1=0.98kg的靶盒A静止在光滑水平面上,水平轻质弹簧一端栓在质量m2=1.0kg的滑块B上,另一端与靶盒A连接,有一固定的发射器,它可以瞄准靶盒发射一颗水平速度为v0=10m/s,质量m0=0.02kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求:
如图所示,质量m1=0.98kg的靶盒A静止在光滑水平面上,水平轻质弹簧一端栓在质量m2=1.0kg的滑块B上,另一端与靶盒A连接,有一固定的发射器,它可以瞄准靶盒发射一颗水平速度为v0=10m/s,质量m0=0.02kg的弹丸,当弹丸打入靶盒A后,便留在盒内,碰撞时间极短,不计空气阻力,求: