题目内容
4.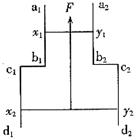 如图所示图中a1b1c1d1和a2b2c2d2为在同一竖直平面内的金属导轨,处在磁感应强度为B的匀强磁场中,磁场方向垂直导轨所在的平面(纸面)向里.导轨的a1b1段与a2b2段是竖直的,距离为l1;c1d1段与c2d2段也是竖直的,距离为l2.x1y1和x2y2为两根质量分别为m1和m2的金属细杆,中间用不可伸长的绝缘轻线相连,两根金属细杆都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R.在金属杆x1y1上施加一个竖直向上的恒力使两杆向上运动.已知两杆运动到图示位置时,以速度v匀速向上运动,求作用于x1y1上的恒力大小?
如图所示图中a1b1c1d1和a2b2c2d2为在同一竖直平面内的金属导轨,处在磁感应强度为B的匀强磁场中,磁场方向垂直导轨所在的平面(纸面)向里.导轨的a1b1段与a2b2段是竖直的,距离为l1;c1d1段与c2d2段也是竖直的,距离为l2.x1y1和x2y2为两根质量分别为m1和m2的金属细杆,中间用不可伸长的绝缘轻线相连,两根金属细杆都垂直于导轨并与导轨保持光滑接触.两杆与导轨构成的回路的总电阻为R.在金属杆x1y1上施加一个竖直向上的恒力使两杆向上运动.已知两杆运动到图示位置时,以速度v匀速向上运动,求作用于x1y1上的恒力大小?
分析 已知两杆以速度v匀速向上运动,整体所受的合外力为零.根据法拉第电磁感应定律、欧姆定律求出两杆所受的安培力,再由平衡条件求解.
解答 解:由法拉第电磁感应定律,回路中的感应电动势的大小:E=B(l2-l1)v
感应电流沿着顺时针方向,回路中的电流大小 I=$\frac{E}{R}$
作用于杆x1y1上的安培力方向向上,大小为 F1=BIl1
作用于杆x2y2上的安培力方向向下,大小为 F2=BIl2.
当金属杆作匀速运动时,两杆受合力为0,则得:
F-m1g-m2g+F1-F2=0
联立以上各式,解得:F=(m1+m2)g+$\frac{{B}^{2}({l}_{1}-{l}_{2})^{2}v}{R}$
答:作用于x1y1上的恒力大小为(m1+m2)g+$\frac{{B}^{2}({l}_{1}-{l}_{2})^{2}v}{R}$.
点评 这是一道电磁感应中的综合题,对于这类题目要弄清回路中的安培力的方向,求得安培力大小,然后根据平衡或牛顿第二定律求解.

练习册系列答案
相关题目
15.对于相隔一定距离的两个质点,要使它们之间的万有引力变为原来的2倍,可行的是( )
| A. | 仅把某质点的质量增大为原来的2倍 | |
| B. | 仅把两者的质量都增大为原来的2倍 | |
| C. | 仅把两者之间的距离减小到原来的$\frac{1}{2}$ | |
| D. | 仅把两者之间的距离减小到原来的$\frac{\sqrt{2}}{2}$ |
12.下列说法正确的是( )
| A. | 光在介质中传播的速度仅由介质本身所决定 | |
| B. | 雨后路面上的油膜形成的彩色条纹是由光的干涉形成的 | |
| C. | 杨氏双缝干涉实验中,当两缝间的距离以及双缝和屏的距离一定时,红光干涉条纹的相邻条纹间距比蓝光干涉条纹的相邻条纹间距小 | |
| D. | 光的偏振特征说明光是横波 |
19. 如图所示,子弹水平射入放在光滑水平地面上静止的木块,子弹未穿透木块,此过程中木块动能增加了5J,那么此过程中系统产生的内能可能为( )
如图所示,子弹水平射入放在光滑水平地面上静止的木块,子弹未穿透木块,此过程中木块动能增加了5J,那么此过程中系统产生的内能可能为( )
 如图所示,子弹水平射入放在光滑水平地面上静止的木块,子弹未穿透木块,此过程中木块动能增加了5J,那么此过程中系统产生的内能可能为( )
如图所示,子弹水平射入放在光滑水平地面上静止的木块,子弹未穿透木块,此过程中木块动能增加了5J,那么此过程中系统产生的内能可能为( )| A. | 16J | B. | 11.2J | C. | 5.6J | D. | 3.4J |
16. 用长L的轻悬线将小球系于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,若无初速度释放小球,当悬线碰到钉子后的瞬间(设线没有断)( )
用长L的轻悬线将小球系于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,若无初速度释放小球,当悬线碰到钉子后的瞬间(设线没有断)( )
 用长L的轻悬线将小球系于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,若无初速度释放小球,当悬线碰到钉子后的瞬间(设线没有断)( )
用长L的轻悬线将小球系于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,若无初速度释放小球,当悬线碰到钉子后的瞬间(设线没有断)( )| A. | 小球的线速度突然增大 | B. | 小球的角速度突然增大 | ||
| C. | 小球的向心加速度突然增大 | D. | 小球受到绳子的拉力突然减小 |
14. 一个物理兴趣小组设计了如图所示的装置,观察闭合铜线圈在蹄形磁铁之间摆动,若不考虑空气阻力,下列说法不正确的是( )
一个物理兴趣小组设计了如图所示的装置,观察闭合铜线圈在蹄形磁铁之间摆动,若不考虑空气阻力,下列说法不正确的是( )
 一个物理兴趣小组设计了如图所示的装置,观察闭合铜线圈在蹄形磁铁之间摆动,若不考虑空气阻力,下列说法不正确的是( )
一个物理兴趣小组设计了如图所示的装置,观察闭合铜线圈在蹄形磁铁之间摆动,若不考虑空气阻力,下列说法不正确的是( )| A. | 线圈在磁铁之间可能做等幅摆动 | |
| B. | 线圈在磁铁之间摆动过程中受到一定受到安培力作用 | |
| C. | 线圈在磁铁之间摆动过程中一定产生感应电流 | |
| D. | 线圈在磁铁之间摆动过程中一定有机械能转化为内能 |
 有界匀强磁场边界线SP平行于MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场.其中穿过a点的粒子速度v1与MN垂直;穿过b点的粒子速度v2与MN成60°角,设两粒子从S到a、b所需时间分别为t1和t2,(重力不计)则t1:t2为多少?v1:v2多少?
有界匀强磁场边界线SP平行于MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场.其中穿过a点的粒子速度v1与MN垂直;穿过b点的粒子速度v2与MN成60°角,设两粒子从S到a、b所需时间分别为t1和t2,(重力不计)则t1:t2为多少?v1:v2多少?



