题目内容
13. 如图,一个小球从地面竖直上抛,不计空气阻力,已知小球两次经过一个较低点A的时间间隔为TA,两次经过较高点B的时间间隔为TB,则A、B两点间的距离为( )
如图,一个小球从地面竖直上抛,不计空气阻力,已知小球两次经过一个较低点A的时间间隔为TA,两次经过较高点B的时间间隔为TB,则A、B两点间的距离为( )| A. | $\frac{g({T}_{A}-{T}_{B})^{2}}{4}$ | B. | $\frac{g({{T}_{A}}^{2}-{{T}_{B}}^{2})}{2}$ | C. | $\frac{g({{T}_{A}}^{2}-{{T}_{B}}^{2})}{4}$ | D. | $\frac{g({{T}_{A}}^{2}-{{T}_{B}}^{2})}{8}$ |
分析 竖直上抛运动具有对称性,利用对称性可以得到物体从顶点到A的时间和从顶点到B点的时间,再由自由落体的规律求解.
解答 解:根据竖直上抛运动的对称,可知物体从顶点下落A点的时间为$\frac{{T}_{A}}{2}$,从顶点下落到B点的时间为$\frac{{T}_{B}}{2}$
而下落过程物体做自由落体运动,则A、B两点间的距离为:
h=$\frac{1}{2}g(\frac{{T}_{A}}{2})^{2}$-$\frac{1}{2}g(\frac{{T}_{B}}{2})^{2}$=$\frac{g({T}_{A}^{2}-{T}_{B}^{2})}{8}$
故选:D.
点评 竖直上抛运动上升和下降具有对称性,所需的时间是一样的,所以只要讨论下落过程就可以.在解题时我们要充分利用对称性.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
3.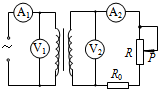 如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )
如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )
 如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )
如图所示为模拟街头变压器通过降压给用户供电的示意图,变压器输入的交流电压可视为不变.变压器输出的低压交流电通过输电线输送给用户.定值电阻R0表示输电线的电阻,变阻器R表示用户用电器的总电阻.若变压器为理想变压器,电表为理想电表,则在变阻器的滑片P向上移动的过程中( )| A. | V2示数变小 | B. | V1示数变大 | C. | A2示数变大 | D. | A1示数变小 |
1.在一次观察光的衍射实验中,观察到如图所示的清晰的亮暗相间的图样,那么障碍物是下列给出的 ( )


| A. | 很小的不透明圆板 | B. | 很大的中间有大圆孔的不透明挡板 | ||
| C. | 很大的不透明圆板 | D. | 很大的中间有小圆孔的不透明挡板 |
8.用某单色光照射金属表面,金属表面有光电子飞出.若照射光的频率增大,强度减弱,则单位时间内飞出金属表面的光电子的( )
| A. | 能量增大,数量增多 | B. | 能量减小,数量减少 | ||
| C. | 能量增大,数量减小 | D. | 能量减小,数量增多 |
18.以不同初速度将两个物体同时竖直向上抛出并开始计时,一个物体所受空气阻力可以忽略,另一个物体所受空气阻力大小与物体速率成正比,下列用虚线和实线描述两物体运动的v-t图象可能正确的是( )
| A. |  | B. |  | C. |  | D. |  |
14. 一箱土豆在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的土豆质量为m,它到转轴的距离为R,则其他土豆对该土豆的作用力为( )
一箱土豆在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的土豆质量为m,它到转轴的距离为R,则其他土豆对该土豆的作用力为( )
 一箱土豆在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的土豆质量为m,它到转轴的距离为R,则其他土豆对该土豆的作用力为( )
一箱土豆在转盘上随转盘以角速度ω做匀速圆周运动,其中一个处于中间位置的土豆质量为m,它到转轴的距离为R,则其他土豆对该土豆的作用力为( )| A. | mg | B. | $\sqrt{{m}^{2}{g}^{2}-{m}^{2}{ω}^{4}{R}^{2}}$ | C. | mω2R | D. | $\sqrt{{m}^{2}{g}^{2}+{m}^{2}{ω}^{4}{R}^{2}}$ |
 如图所示,在倾角θ=37°的绝缘斜面所在空间存在着竖直向上的匀强电场,场强E=4.0×103N/C,在斜面底端有一与斜面垂直的绝缘弹性挡板.质量m=0.20kg的带电滑块从斜面顶端由静止开始滑下,滑到斜面底端以与挡板相碰前的速率返回.已知斜面的高度h=0.24m,滑块与斜面间的动摩擦因数μ=0.30,滑块带电荷q=-5.0×10-4C,取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.求:
如图所示,在倾角θ=37°的绝缘斜面所在空间存在着竖直向上的匀强电场,场强E=4.0×103N/C,在斜面底端有一与斜面垂直的绝缘弹性挡板.质量m=0.20kg的带电滑块从斜面顶端由静止开始滑下,滑到斜面底端以与挡板相碰前的速率返回.已知斜面的高度h=0.24m,滑块与斜面间的动摩擦因数μ=0.30,滑块带电荷q=-5.0×10-4C,取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.求: 如图,某地球卫星在轨道上运动,每经过时间t通过的轨道弧长为l、扫过的圆心角为θ(弧度).该卫星的周期为$\frac{2πt}{θ}$,地球的质量为$\frac{{l}^{3}}{G{t}^{2}θ}$.(已知引力常量为G)
如图,某地球卫星在轨道上运动,每经过时间t通过的轨道弧长为l、扫过的圆心角为θ(弧度).该卫星的周期为$\frac{2πt}{θ}$,地球的质量为$\frac{{l}^{3}}{G{t}^{2}θ}$.(已知引力常量为G) 一定质量的理想气体由状态A变为状态C,其有关数据如图所示.若状态C的压强是105Pa,求:
一定质量的理想气体由状态A变为状态C,其有关数据如图所示.若状态C的压强是105Pa,求: