题目内容
3. 如图所示,线圈L的自感系数为25mH,电阻为零,电容器C的电容为40 μF,灯泡D的规格是“4V、2W”.开关S闭合后,灯泡正常发光,S断开后,LC中产生振荡电流.若从S断开开始计时,求:
如图所示,线圈L的自感系数为25mH,电阻为零,电容器C的电容为40 μF,灯泡D的规格是“4V、2W”.开关S闭合后,灯泡正常发光,S断开后,LC中产生振荡电流.若从S断开开始计时,求:(1)当t=$\frac{π}{2}$×10 -3s时,电容器的右极板带何种电荷;
(2)当t′=π×10 -3s时,LC回路中的电流.
分析 (1)根据T=$2π\sqrt{LC}$,即可求解振荡周期;再结合电容器的充电与放电时间与周期关系,从而即可求解.
(2)根据电容器的充电与放电时间与周期关系,结合欧姆定律即可求出.
解答 解:(1)根据T=$2π\sqrt{LC}$,可求得周期为:T=$2π×\sqrt{25×1{0}^{-3}×40×1{0}^{-6}}=2π×1{0}^{-3}$s.
由图可知,当电路中的电流稳定时,电容器两端的电压等于0,所以在电流稳定后断开S后,由于电容器与电感线圈串联组成振荡回路,所以电容器开始充电.
由于:t=$\frac{π}{2}$×10 -3s=$\frac{T}{4}$
可知t时刻恰好充电完毕.
由于开始时流过线圈的电流的方向向右,所以S闭合后电容器C的右端先充入正电荷,即在t=$\frac{π}{2}$×10 -3s时,电容器的右极板带正电荷.
(2)由t′=π×10 -3s=$\frac{1}{2}$T,开始在t′时刻振荡回路中的电流与开始时的电流大小相等,方向相反.
开始时的电流:$I=\frac{P}{U}=\frac{2}{4}=0.5$A
答:(1)当t=$\frac{π}{2}$×10 -3s时,电容器的右极板带正电荷;
(2)当t′=π×10 -3s时,LC回路中的电流是0.5 A
点评 该题考查振荡电路产生的振荡电流周期公式,理解充电与放电过程,电量,电场强度,电压,电流的大小如何变化.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
13. 如图所示,放在水平地面上的物体a上叠放着物体b,a和b间用轻质弹簧相连,已知弹簧处于压缩状态,整个装置处于静止状态,则关于a、b的受力分析正确的是( )
如图所示,放在水平地面上的物体a上叠放着物体b,a和b间用轻质弹簧相连,已知弹簧处于压缩状态,整个装置处于静止状态,则关于a、b的受力分析正确的是( )
 如图所示,放在水平地面上的物体a上叠放着物体b,a和b间用轻质弹簧相连,已知弹簧处于压缩状态,整个装置处于静止状态,则关于a、b的受力分析正确的是( )
如图所示,放在水平地面上的物体a上叠放着物体b,a和b间用轻质弹簧相连,已知弹簧处于压缩状态,整个装置处于静止状态,则关于a、b的受力分析正确的是( )| A. | b受到向左的摩擦力 | B. | a受到b对它的向左的摩擦力 | ||
| C. | 地面对a的摩擦力向右 | D. | 地面对a无摩擦力作用 |
14. 在2016年里约奥运会体操男子吊环决赛中,当地时间8月15日,希腊名将以佩特鲁尼亚斯以16.000的高分获得冠军.如图为比赛中某个时刻的模拟图,运动员静止不动,两根吊带对称并于竖直方向有一定夹角.此时左、右两根吊带对称并与竖直方向有一定夹角.此时左、右两吊环对运动员的作用力大小分别为F1、F2,则下列判断正确的是( )
在2016年里约奥运会体操男子吊环决赛中,当地时间8月15日,希腊名将以佩特鲁尼亚斯以16.000的高分获得冠军.如图为比赛中某个时刻的模拟图,运动员静止不动,两根吊带对称并于竖直方向有一定夹角.此时左、右两根吊带对称并与竖直方向有一定夹角.此时左、右两吊环对运动员的作用力大小分别为F1、F2,则下列判断正确的是( )
 在2016年里约奥运会体操男子吊环决赛中,当地时间8月15日,希腊名将以佩特鲁尼亚斯以16.000的高分获得冠军.如图为比赛中某个时刻的模拟图,运动员静止不动,两根吊带对称并于竖直方向有一定夹角.此时左、右两根吊带对称并与竖直方向有一定夹角.此时左、右两吊环对运动员的作用力大小分别为F1、F2,则下列判断正确的是( )
在2016年里约奥运会体操男子吊环决赛中,当地时间8月15日,希腊名将以佩特鲁尼亚斯以16.000的高分获得冠军.如图为比赛中某个时刻的模拟图,运动员静止不动,两根吊带对称并于竖直方向有一定夹角.此时左、右两根吊带对称并与竖直方向有一定夹角.此时左、右两吊环对运动员的作用力大小分别为F1、F2,则下列判断正确的是( )| A. | F1、F2是一对作用力和反作用力 | |
| B. | 两个吊环对运动员的作用力的合力一定竖直向上 | |
| C. | 每根吊带受到吊环的拉力的大小都等于运动员重力的一半 | |
| D. | 在运动员将两吊带再缓慢向两边撑开的过程中,吊带上的张力缓慢增大 |
18.下列关于惯性的说法正确的是( )
| A. | 子弹由于速度大,所以惯性就大 | |
| B. | 百米赛跑到终点不能立即停下是由于惯性,停下是就没有惯性了 | |
| C. | 急刹车时,车上的乘客由于惯性一样大,所以都会向前倾倒 | |
| D. | 质量大的物体运动状态不容易改变,是由于物体的质量大,惯性也就大的缘故 |
8.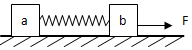 如图,在水平面上放着两个木块a和b,质量分别为ma,mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a,b以相同的速度做匀速直线运动,弹簧的伸长量x.则下列关系正确的是( )
如图,在水平面上放着两个木块a和b,质量分别为ma,mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a,b以相同的速度做匀速直线运动,弹簧的伸长量x.则下列关系正确的是( )
 如图,在水平面上放着两个木块a和b,质量分别为ma,mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a,b以相同的速度做匀速直线运动,弹簧的伸长量x.则下列关系正确的是( )
如图,在水平面上放着两个木块a和b,质量分别为ma,mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a,b以相同的速度做匀速直线运动,弹簧的伸长量x.则下列关系正确的是( )| A. | 弹簧对a物体的弹力小于对b物体的弹力 | |
| B. | a受到的弹簧的拉力为F-μmbg | |
| C. | b物体在水平方向只受两个力的作用 | |
| D. | a、b之间的距离为L+$\frac{μmag}{k}$ |
12. 将软木板挂在竖直墙壁上作为镖靶.在离墙壁一定距离的同一处,将两只飞镖水平掷出,不计空气阻力,如图,则( )
将软木板挂在竖直墙壁上作为镖靶.在离墙壁一定距离的同一处,将两只飞镖水平掷出,不计空气阻力,如图,则( )
 将软木板挂在竖直墙壁上作为镖靶.在离墙壁一定距离的同一处,将两只飞镖水平掷出,不计空气阻力,如图,则( )
将软木板挂在竖直墙壁上作为镖靶.在离墙壁一定距离的同一处,将两只飞镖水平掷出,不计空气阻力,如图,则( )| A. | A掷出时的初速度一定比B大 | B. | B插入靶时的末速度一定比A大 | ||
| C. | B运动时间一定比A长 | D. | A的质量一定比B大 |
 用游标卡尺测得某材料的长度如图甲所示,读数L=5.020 cm;用螺旋测微器测得该材料的直径如图乙所示,读数D=2.150 mm.
用游标卡尺测得某材料的长度如图甲所示,读数L=5.020 cm;用螺旋测微器测得该材料的直径如图乙所示,读数D=2.150 mm. 如图所示,一个质量为m0的人,站在台秤(用于测量压力)上,手拿一个质量为m,悬线长为R的小球,使小球在竖直平面内做匀速圆周运动,且小球恰好通过圆轨道的最高点(此时悬线的弹力为0),求小球经过最低点时,台秤的示数多大?
如图所示,一个质量为m0的人,站在台秤(用于测量压力)上,手拿一个质量为m,悬线长为R的小球,使小球在竖直平面内做匀速圆周运动,且小球恰好通过圆轨道的最高点(此时悬线的弹力为0),求小球经过最低点时,台秤的示数多大? 如图所示,静止在水平桌面上的纸带上有一质量为0.1kg的小铁块,它离纸带的右端距离为0.5m,铁块与纸带间动摩擦因数为0.1.现用力向左以2m/s2的加速度将纸带从铁块下抽出,(不计铁块大小,铁块不滚动,取g=10m/s2)则,将纸带从铁块下抽出需要1s;铁块从纸带上掉下来时的动能为0.05J.
如图所示,静止在水平桌面上的纸带上有一质量为0.1kg的小铁块,它离纸带的右端距离为0.5m,铁块与纸带间动摩擦因数为0.1.现用力向左以2m/s2的加速度将纸带从铁块下抽出,(不计铁块大小,铁块不滚动,取g=10m/s2)则,将纸带从铁块下抽出需要1s;铁块从纸带上掉下来时的动能为0.05J.