题目内容
3.轻杆的一端固定在O点,另一端连接一质量为m的小球,小球可随轻杆绕O点在竖直平面内做圆周运动,现在某位置给小球一定的初速度,小球立即绕O点作圆周运动.已知小球到最低点时,杆对小球的拉力为7mg,不计一切摩擦,则小球到最高点时,下列说法正确的是( )| A. | 小球对杆的力为mg,方向竖直向下 | B. | 小球对杆的力为2mg,方向竖直向下 | ||
| C. | 小球对杆的力为mg,方向竖直向上 | D. | 小球对杆恰好没有作用力 |
分析 对小球,先根据牛顿第二定律得到杆对小球的拉力与速度关系式.再根据动能定理求出小球到最高点时的速度,根据牛顿第二定律求出杆对小球作用力的大小和方向,再由牛顿第三定律分析小球对杆的作用力大小和方向.
解答 解:在最低点,对小球,由牛顿第二定律得
T1-mg=m$\frac{{v}_{1}^{2}}{L}$
从最低点到最高点,由动能定理得:
-mg•2L=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12,
在最高点,设杆对小球的作用力大小为T2,方向竖直向下.则有
mg+T2=m$\frac{{v}_{2}^{2}}{L}$
由以上三式解得 T2=mg.方向竖直向下.
由牛顿第三定律得知,小球对杆的力为mg,方向竖直向上.
故选:C
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
19. 如图所示,A、B两球质量均为m.固定在轻弹簧的两端,分别用细绳悬于O点,其中球A处在光滑竖直墙面和光滑水平墙面的交界处,已知两球均处于平衡状态,OAB恰好构成一个正三角形,则下列说法正确的是(重力加速度为g)( )
如图所示,A、B两球质量均为m.固定在轻弹簧的两端,分别用细绳悬于O点,其中球A处在光滑竖直墙面和光滑水平墙面的交界处,已知两球均处于平衡状态,OAB恰好构成一个正三角形,则下列说法正确的是(重力加速度为g)( )
 如图所示,A、B两球质量均为m.固定在轻弹簧的两端,分别用细绳悬于O点,其中球A处在光滑竖直墙面和光滑水平墙面的交界处,已知两球均处于平衡状态,OAB恰好构成一个正三角形,则下列说法正确的是(重力加速度为g)( )
如图所示,A、B两球质量均为m.固定在轻弹簧的两端,分别用细绳悬于O点,其中球A处在光滑竖直墙面和光滑水平墙面的交界处,已知两球均处于平衡状态,OAB恰好构成一个正三角形,则下列说法正确的是(重力加速度为g)( )| A. | 球A一定受到四个力的作用 | |
| B. | 弹簧对球A的弹力大于对球B的弹力 | |
| C. | 绳OA对球A的拉力大小一定等于1.5mg | |
| D. | 绳OB对球B的拉力大小一定等于mg |
4.下面关于碰撞的理解,正确的是( )
| A. | 碰撞是指相对运动的物体相遇时,在极短时间内它们的运动状态发生显著变化的过程 | |
| B. | 在碰撞现象中,一般来说物体所受的外力作用不能忽略 | |
| C. | 如果碰撞过程中动能不变,则这样的碰撞叫做非弹性碰撞 | |
| D. | 根据碰撞过程中动能是否守恒,碰撞可分为正碰和斜碰 |
14. 如图所示,某交流发电机的线圈共n匝,面积为S,内阻为r,线圈两端与R的电阻构成闭合回路.当线圈在磁感应强度为B的匀强磁场中,以角速度ω绕轴OO'匀速转动时,下列说法不正确的是( )
如图所示,某交流发电机的线圈共n匝,面积为S,内阻为r,线圈两端与R的电阻构成闭合回路.当线圈在磁感应强度为B的匀强磁场中,以角速度ω绕轴OO'匀速转动时,下列说法不正确的是( )
 如图所示,某交流发电机的线圈共n匝,面积为S,内阻为r,线圈两端与R的电阻构成闭合回路.当线圈在磁感应强度为B的匀强磁场中,以角速度ω绕轴OO'匀速转动时,下列说法不正确的是( )
如图所示,某交流发电机的线圈共n匝,面积为S,内阻为r,线圈两端与R的电阻构成闭合回路.当线圈在磁感应强度为B的匀强磁场中,以角速度ω绕轴OO'匀速转动时,下列说法不正确的是( )| A. | 从图示位置转过90°的过程中,通过电阻R横截面的电荷量q=$\frac{nBS}{R}$ | |
| B. | 产生感应电动势的有效值E=$\frac{nBSω}{{\sqrt{2}}}$ | |
| C. | 线圈经过中性面时,感应电流达到了最小值 | |
| D. | 线圈中的电流每经过时间$\frac{π}{ω}$方向改变一次 |
10. 如图为处于静电场中某空腔导体周围的电场分布情况,实线表示电场线,虚线表示等势面.A、B、C为电场中的三个点,O为空腔导体内的一点.下列说法正确的是( )
如图为处于静电场中某空腔导体周围的电场分布情况,实线表示电场线,虚线表示等势面.A、B、C为电场中的三个点,O为空腔导体内的一点.下列说法正确的是( )
 如图为处于静电场中某空腔导体周围的电场分布情况,实线表示电场线,虚线表示等势面.A、B、C为电场中的三个点,O为空腔导体内的一点.下列说法正确的是( )
如图为处于静电场中某空腔导体周围的电场分布情况,实线表示电场线,虚线表示等势面.A、B、C为电场中的三个点,O为空腔导体内的一点.下列说法正确的是( )| A. | A点的电势比B点的电势高 | |
| B. | A点的电场强度小于B点的电场强度 | |
| C. | 导体表面的电场线与导体表面不垂直 | |
| D. | 将正电荷从A点移到C点,电场力做正功 |
 在《验证力的平行四边形定则》实验中,某同学首先将白纸固定在方木板上,将橡皮筋的一端固定在木板上的A点,另一端拴上两根细绳,每根细绳分别连着一个量程为5N、最小刻度为0.1N的弹簧测力计,然后沿着两个不同的方向拉弹簧测力计,如图所示,夹角α+β=90°.
在《验证力的平行四边形定则》实验中,某同学首先将白纸固定在方木板上,将橡皮筋的一端固定在木板上的A点,另一端拴上两根细绳,每根细绳分别连着一个量程为5N、最小刻度为0.1N的弹簧测力计,然后沿着两个不同的方向拉弹簧测力计,如图所示,夹角α+β=90°. 某学习小组在验证动量守恒定律的实验中设计了如图所示的实验装置,上表面光滑的长木板固定在水平地面上,木板上有两个质量均为M的小车,其中小车A车以速度2v0向右运动,而小车B以v0速度向左运动,两小车碰撞时瞬间连成一个整体继续向右运动,并以一定的速度接触右侧的减振装置,两小车与减振装置相互作用的时间为t,且与减振装置作用时无机械能损失,求:
某学习小组在验证动量守恒定律的实验中设计了如图所示的实验装置,上表面光滑的长木板固定在水平地面上,木板上有两个质量均为M的小车,其中小车A车以速度2v0向右运动,而小车B以v0速度向左运动,两小车碰撞时瞬间连成一个整体继续向右运动,并以一定的速度接触右侧的减振装置,两小车与减振装置相互作用的时间为t,且与减振装置作用时无机械能损失,求: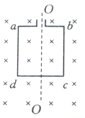 如图所示为交流发电机模型,矩形线圈abcd绕oo’轴在匀强磁场中匀速转动.已知线圈共有100匝,图示位置线圈平面与磁场垂直,穿过线圈的磁通量为0.02wb,经0.5s线圈转动900,则上述转动过程中穿过线圈磁通量减小(填变大、变小或不变),线圈中产生的感应电动势为4V.
如图所示为交流发电机模型,矩形线圈abcd绕oo’轴在匀强磁场中匀速转动.已知线圈共有100匝,图示位置线圈平面与磁场垂直,穿过线圈的磁通量为0.02wb,经0.5s线圈转动900,则上述转动过程中穿过线圈磁通量减小(填变大、变小或不变),线圈中产生的感应电动势为4V.