题目内容
19. 如图所示,水平传送带以v=2m/s的速率沿逆时针方向转动,在其左端与一竖直固定的光滑轨道平滑相接,右端与一半径R=0.4m的光滑半圆轨道相切,一质量m=2kg的物块(可视为质点)从光滑轨道上的某点由静止开始下滑,通过水平传送带后从半圆轨道的最高点水平抛出,并恰好落在传送带的最左端,已知物块通过半圆轨道最高点时受到的弹力F=60N,物块与传送带间的动摩擦因数μ=0.25,取重力加速度g=10m/s2,求:(计算结果可以保留根号)
如图所示,水平传送带以v=2m/s的速率沿逆时针方向转动,在其左端与一竖直固定的光滑轨道平滑相接,右端与一半径R=0.4m的光滑半圆轨道相切,一质量m=2kg的物块(可视为质点)从光滑轨道上的某点由静止开始下滑,通过水平传送带后从半圆轨道的最高点水平抛出,并恰好落在传送带的最左端,已知物块通过半圆轨道最高点时受到的弹力F=60N,物块与传送带间的动摩擦因数μ=0.25,取重力加速度g=10m/s2,求:(计算结果可以保留根号)(1)物块作平抛运动的初速度v0;
(2)水平传送带的长度;
(3)电动机由于物块通过传送带而多消耗的电能E.
分析 (1)物块在最高点受到的重力和弹力提供向心力,由牛顿第二定律即可求出物块作平抛运动的初速度v0;
(2)物块从最高点开始做平抛运动,结合平抛运动的特点求出水平距离,由图可知,该距离即为传送带的长度;
(3)分析判断物快在皮带的运动情况,求出物块在传送带上滑行的时间以及传送带的位移;最后利用能量守恒求多提供的能量.
解答 解:(1)物块在最高点受到的重力和弹力提供向心力,由牛顿第二定律得:
mg+F=m$\frac{{v}_{0}^{2}}{R}$
代入数据得:v0=4m/s
(2)物块离开最高点后做平抛运动,由:h=$\frac{1}{2}$gt2;
得运动的时间:t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×2R}{g}}$=2$\sqrt{\frac{0.4}{10}}$s=0.4s
物块沿水平方向平抛的距离:L=v0t=4×0.4=1.6m
由题可知,传送带的长度也是1.6m
(3)物块在整个运动的过程中,重力和传送带的摩擦力做功,由动能定理得:
mg(H-2R)-μmgL=$\frac{1}{2}m{v}_{0}^{2}$
代入数据得:H=2m
物块到达传送带的左端的过程中重力做功,由机械能守恒得:
mgH=$\frac{1}{2}m{v}_{1}^{2}$
得:v1=$\sqrt{2gH}$=$\sqrt{2×10×2}$=2$\sqrt{10}$m/s
物块在传送带上运动的加速度大小:a=$\frac{μmg}{m}$=μg=0.25×10=2.5m/s2;
物块经过传送带的时间t′,则:
L=v1t′-$\frac{1}{2}$at′2;
该时间内传送带运动的距离:L′=v1t′
传送带克服摩擦力做的功:W=fL′=μmgL′
根据能量转化的方向可知,电动机由于物块通过传送带而多消耗的电能E等于传送带克服物块的摩擦力做的功,即:
E=W
联立以上各式,代入数据解得:E=8($\sqrt{10}$-2$\sqrt{2}$)J≈3J
答:
(1)物块作平抛运动的初速度是4m/s;
(2)水平传送带的长度是1.6m;
(3)电动机由于物块通过传送带而多消耗的电能是3J.
点评 该题结合平抛运动和机械能守恒考查传送带问题,判断物快在皮带上的运动情况是关键,灵活应用机械能、平抛运动和能量守恒定律是解题的核心.

| A. | 电动机线圈产生的热量为I2Rt | B. | 电动机线圈产生的热量为$\frac{{U}^{2}t}{R}$ | ||
| C. | 电动机消耗的电能为$\frac{{U}^{2}t}{R}$ | D. | 电动机输出的机械能为UIt |
 据英国《每日邮报》2015年3月6日报道,“格利泽581d”行星大小约为地球的3倍,是人类在太阳系之外发现的第一个位于宜居带中的行星,被称为“超级地球”.它距离地球22光年,在浩瀚的宇宙中算得上是“邻居”.在以“格利泽581”为中心绕转的多颗行星中,“格利泽581c”“格利泽581d”分别与“格利泽581”的距离之比为7:22,则这两颗行星( )
据英国《每日邮报》2015年3月6日报道,“格利泽581d”行星大小约为地球的3倍,是人类在太阳系之外发现的第一个位于宜居带中的行星,被称为“超级地球”.它距离地球22光年,在浩瀚的宇宙中算得上是“邻居”.在以“格利泽581”为中心绕转的多颗行星中,“格利泽581c”“格利泽581d”分别与“格利泽581”的距离之比为7:22,则这两颗行星( )| A. | 格利泽581d的周期大 | B. | 格利泽581d的线速度大 | ||
| C. | 格利泽581d的角速度大 | D. | 格利泽581d的向心加速度大 |
| A. | “天宫一号”的动能比“天宫二号”的动能大 | |
| B. | “天宫一号”的周期比“天宫二号”的周期小 | |
| C. | “神舟十一号”飞船的环绕速度大于第一宇宙速度 | |
| D. | “神舟十一号”飞船必须在“天宫二号”的轨道上,再加速实现对接 |
| A. | $\frac{{{a_1}{t_1}+{a_2}{t_2}}}{4}$ | B. | $\frac{{{a_2}{t_2}}}{2}$ | ||
| C. | $\frac{{{a_1}{t_1}^2+{a_2}{t_2}^2}}{{2({{t_1}+{t_2}})}}$ | D. | $\frac{{{a_1}{t_1}+{a_2}{t_2}}}{2}$ |
| A. | 欧姆 | B. | 安培 | C. | 奥斯特 | D. | 特斯拉 |
| A. | 1.2 A | B. | 0.8 A | C. | 0.4 A | D. | 0 |
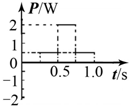
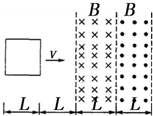 光滑的水平桌面上方存在宽度均为L=0.5m、磁感应强度均为B=1T的两个方向相反的有界匀强磁场,磁场方向分别竖直向下和向上,如图所示.在磁场区域的左侧有一边长L=0.5m的正方形导体线框,线框右侧距磁场边界也为L=0.5m,线框总电阻为R=2Ω.现使线框沿桌面以v=2m/s的速度匀速穿过磁场区域,规定线框中逆时针方向的电流和电动势为正方向,磁通量方向向下为正方向.则关于线框中的感应电动势、感应电流、电功率和穿过线框的磁通量的下列图象正确的是( )
光滑的水平桌面上方存在宽度均为L=0.5m、磁感应强度均为B=1T的两个方向相反的有界匀强磁场,磁场方向分别竖直向下和向上,如图所示.在磁场区域的左侧有一边长L=0.5m的正方形导体线框,线框右侧距磁场边界也为L=0.5m,线框总电阻为R=2Ω.现使线框沿桌面以v=2m/s的速度匀速穿过磁场区域,规定线框中逆时针方向的电流和电动势为正方向,磁通量方向向下为正方向.则关于线框中的感应电动势、感应电流、电功率和穿过线框的磁通量的下列图象正确的是( )