题目内容
如图(a)所示,真空中半径为R的圆形区域内存在匀强磁场,磁场方向垂直纸面向外,磁场右侧有一对平行金属板M和N,两板间的距离为R,板长为2R,板的中心线O1O2与磁场的圆心O在同一直线上,有一电荷量为q、质量为m的带正电的粒子,以速度v0由圆周上的a点沿垂直于半径OO1并指向圆心O的方向进入磁场,当从圆周上的O1点沿OO1方向飞出磁场时,给出M、N板加上如图(b)所示电压,最后粒子刚好以平行于N板的速度,从N板的边缘飞出(不计粒子重力).求:
(1)磁场的磁感应强度B;
(2)交变电压的周期T和电压U0的值.

(1)磁场的磁感应强度B;
(2)交变电压的周期T和电压U0的值.

分析:(1)根据洛伦兹力提供向心力,结合牛顿第二定律,即可求解;
(2)由粒子自O1点进入电场,最后恰好从N的边缘平行极板飞出,则竖直方向速度刚好为零,根据周期公式与运动学公式,即可求解.
(2)由粒子自O1点进入电场,最后恰好从N的边缘平行极板飞出,则竖直方向速度刚好为零,根据周期公式与运动学公式,即可求解.
解答:解:(1)粒子自a点进入磁场,从O1点水平飞出磁场,运动的轨道半径为R,
则qBυ0=
①
解得:B=
②
(2)粒子自O1点进入电场,最后恰好从N的边缘平行极板飞出,则竖直方向速度刚好为零,
设运动时间为t,则t=nT(m=1,2,…)③
则沿O1O2方向2R=υ0t④
解得:T=
⑤
沿垂直于O1O2方向;
则有,
=n?2?
(
)2⑥
解得:U0=
(n=1,2,…)
答:(1)磁场的磁感应强度为B=
;
(2)交变电压的周期T和电压U0的值为:U0=
(n=1,2,…).
则qBυ0=
m
| ||
| R |
解得:B=
| mυ0 |
| qR |
(2)粒子自O1点进入电场,最后恰好从N的边缘平行极板飞出,则竖直方向速度刚好为零,
设运动时间为t,则t=nT(m=1,2,…)③
则沿O1O2方向2R=υ0t④
解得:T=
| 2R |
| nυ0 |
沿垂直于O1O2方向;
则有,
| R |
| 2 |
| 1 |
| 2 |
| qU0 |
| mR |
| T |
| 2 |
解得:U0=
nm
| ||
| 2q |
答:(1)磁场的磁感应强度为B=
| mυ0 |
| qR |
(2)交变电压的周期T和电压U0的值为:U0=
nm
| ||
| 2q |
点评:考查粒子在磁场中做匀速圆周运动,在电场中做类平抛运动,掌握处理两种运动的方法,理解牛顿第二定律与运动学公式的综合应用,注意运动的周期性.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 磁体和电流之间、磁体和运动电荷之间、电流和电流之间都可通过磁场而相互作用,此现象可通过以下实验证明:
磁体和电流之间、磁体和运动电荷之间、电流和电流之间都可通过磁场而相互作用,此现象可通过以下实验证明: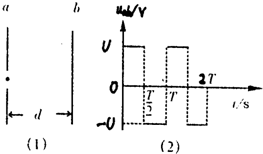 如图(1)所示,真空中足够大的两个互相平行的金属板a、b之间的距离为d,两板之间的电压按如图(2)所示的规律做周期性的变化(当a比b电势高时,电压为正,当a比b电势低时,电压为负),其电压变化周期为T,电压的最大值为U.一个质量为m、电荷量为q的带正电粒子(重力不计)在电场力的作用下,在t=
如图(1)所示,真空中足够大的两个互相平行的金属板a、b之间的距离为d,两板之间的电压按如图(2)所示的规律做周期性的变化(当a比b电势高时,电压为正,当a比b电势低时,电压为负),其电压变化周期为T,电压的最大值为U.一个质量为m、电荷量为q的带正电粒子(重力不计)在电场力的作用下,在t= 一束细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示,求此透明体的临界角和折射率.
一束细光束由真空沿着径向射入一块半圆柱形透明体,如图(a)所示,对其射出后的折射光线的强度进行记录,发现折射光线的强度随着θ的变化而变化,如图(b)的图线所示,求此透明体的临界角和折射率.