题目内容
11．如图所示，做匀加速直线运动的质点，通过某一段距离x的时间为t1，通过下一段同样长距离x的时间为t2，求质点的加速度．
分析 匀变速直线运动某段时间内的平均速度等于中间时刻的瞬时速度，根据平均速度公式即可求出两时间段内的中间时刻速度，再由速度公式即可求得平均速度．
解答 解：分别对两段求平均速度，再根据平均速度等于中间时刻的瞬时速度可知，
AB中点的瞬时速度v1=$\frac{x}{{t}_{1}}$；
BC中点的平均速度v2=$\frac{x}{{t}_{2}}$
两中点的时间间隔为$\frac{{t}_{1}+{t}_{2}}{2}$
由速度公式可得：
a=$\frac{{v}_{2}-{v}_{1}}{\frac{{t}_{1}+{t}_{2}}{2}}$=$\frac{x（{t}_{1}-{t}_{2}）}{{t}_{1}{t}_{2}（{t}_{1}+{t}_{2}）}$
答：质点的加速度为$\frac{x（{t}_{1}-{t}_{2}）}{{t}_{1}{t}_{2}（{t}_{1}+{t}_{2}）}$
点评 本题考查匀变速直线运动规律的应用问题，要注意平均速度公式的应用非常广泛，在解题中一定要注意正确应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．一汽车从静止开始匀加速开出，然后保持匀速运动，最后匀减速运动直到停止．从汽车开始运动起计时，下表给出了某些时刻汽车的瞬时速度．由表中的数据通过分析、计算可得出（ ）
| 时刻（s） | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
| 速度（m/s） | 3.0 | 6.0 | 9.0 | 12 | 12 | 9.0 | 3.0 |
| A． | 汽车加速运动经历的时间为3 s | |
| B． | 汽车加速运动经历的时间为5 s | |
| C． | 汽车匀速运动的时间为2 s | |
| D． | 汽车减速运动的加速度大小为6 m/s2 |
2．
如图所示，质量为m的小球用一根细线和一根轻弹簧悬挂起来，小球静止时，细线水平，而弹簧与竖直成θ角．现将细线剪断，则下列判断正确的是（ ）
如图所示，质量为m的小球用一根细线和一根轻弹簧悬挂起来，小球静止时，细线水平，而弹簧与竖直成θ角．现将细线剪断，则下列判断正确的是（ ）| A． | 剪断细线前，细线中张力为$\frac{mg}{tanθ}$ | |
| B． | 剪断细线前，弹簧弹力大小为$\frac{mg}{cosθ}$ | |
| C． | 剪断细线瞬间，小球所受合力大小为mgsinθ | |
| D． | 剪断细线瞬间，小球所受合力大小为mgtanθ |
9．一物体从长为L的光滑斜面的顶端由静止开始匀加速滑下，经时间t滑到底端，则下列说法正确的是（ ）
| A． | 物体运动到底端时的速度是$\frac{L}{t}$ | |
| B． | 物体在斜面上运动的中间时刻的即时速度是$\frac{L}{2t}$ | |
| C． | 物体运动到斜面中点时瞬时速度是$\frac{\sqrt{2}L}{t}$ | |
| D． | 物体从顶点运动到斜面中点所需的时间是$\frac{\sqrt{2}t}{4}$ |
6．
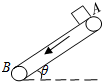如图所示为粮袋的传送装置，已知AB间长度为L，传送带与水平方向的夹角为θ，工作时运行速度为v，粮袋与传送带间的动摩擦因数为μ，正常工作时工人在A点将粮袋放到运行中的传送带上，关于粮袋从A到B的运动，以下说法正确的是（设最大静摩擦力等于滑动摩擦力）（ ）
如图所示为粮袋的传送装置，已知AB间长度为L，传送带与水平方向的夹角为θ，工作时运行速度为v，粮袋与传送带间的动摩擦因数为μ，正常工作时工人在A点将粮袋放到运行中的传送带上，关于粮袋从A到B的运动，以下说法正确的是（设最大静摩擦力等于滑动摩擦力）（ ）| A． | 粮袋到达B点的速度与v比较，可能比v大，也可能与v相等或比v小 | |
| B． | 粮袋开始运动的加速度为g（sinθ-cosθ），若L足够大，则以后将一定以速度v做匀速运动 | |
| C． | 若μ≤tanθ，则粮袋从A到B一定一直是做加速运动 | |
| D． | 不论μ多大，粮袋从A到B一直匀加速运动，且a＞gsinθ |
一质量为m的物体，置于水平面上，现用与水平方向成θ角斜向上的拉力F去拉物体，如图所示，使物体沿水平面做匀加速直线运动，若物体与地面间的动摩擦因数为μ，求物体的加速度．