题目内容
16. 某电视台的娱乐节目中,有一个拉板块的双人游戏,考验两人的默契度.如图所示,一长L=0.60m、质量M=0.40kg的木板靠在光滑竖直墙面上,木板右下方有一质量m=0.80kg的小滑块(可视为质点),滑块与木板间的动摩擦因数为μ=0.20,滑块与木板间的最大静摩擦力等于滑动摩擦力,取g=10m/s2.一人用水平恒力F1向左作用在滑块上,另一人用竖直恒力F2向上拉动滑块,使滑块从地面由静止开始向上运动.
某电视台的娱乐节目中,有一个拉板块的双人游戏,考验两人的默契度.如图所示,一长L=0.60m、质量M=0.40kg的木板靠在光滑竖直墙面上,木板右下方有一质量m=0.80kg的小滑块(可视为质点),滑块与木板间的动摩擦因数为μ=0.20,滑块与木板间的最大静摩擦力等于滑动摩擦力,取g=10m/s2.一人用水平恒力F1向左作用在滑块上,另一人用竖直恒力F2向上拉动滑块,使滑块从地面由静止开始向上运动.(1)为使木板能向上运动,求F1必须满足什么条件?
(2)若F1=22N,为使滑块与木板能发生相对滑动,求F2必须满足什么条件?
(3)游戏中,如果滑块上移h=1.5m时,滑块与木板没有分离,才算两人配合默契,游戏成功.现F1=24N,F2=16N,请通过计算判断游戏能否成功?
分析 (1)木板靠在光滑的墙壁上,若使木板能向上运动,则物块对木板的摩擦力应大于木板的重力,列出关系式计算可得.
(2)由牛顿第二定律分别求出木板和物块的加速度,若物块的加速度大于木板的加速度即会发生相对滑动.
(3)分别对木板和滑块分析,根据牛顿第二定律求出各自加速度,根据各自加速度求出位移,判断相对滑动的位移,与1.5m作比较,可得出结果.
解答 解:(1)滑块与木板间的滑动摩擦力:f=μF1
对木板应有:f>Mg
代入数据得:F1>20N
(2)对木板由牛顿第二定律有:μF1-Mg=Ma1
对滑块由牛顿第二定律有:F2-μF1-mg=ma2
要能发生相对滑动应有:a2>a1
代入数据可得:F2>13.2N
(3)对滑块由牛顿第二定律有:F2-μF1-mg=ma3
设滑块上升h的时间为t,则:$h=\frac{1}{2}{a_3}{t^2}$
对木板由牛顿第二定律有:μF1-Mg=Ma4
设木板在t时间上升的高度为H,则:$H=\frac{1}{2}{a_4}{t^2}$
代入数据可得:H=0.75m
由于H+L<h,滑块在上升到1.5m之前已经脱离了木板,游戏不能成功.
答:(1)为使木板能向上运动,求F1必须满足F1>20N
(2)若F1=22N,为使滑块与木板能发生相对滑动,求F2必须满足F2>13.2N
(3)游戏不能成功.
点评 本题看起来很复杂,需要细心分析,充分利用牛顿第二定律和运动之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.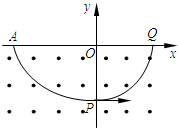 如图所示,直角坐标系xOy位于竖直平面内,y轴竖直向上.第Ⅲ、Ⅳ象限内有垂直于坐标面向外的匀强磁场,第Ⅳ象限同时存在方向平行于y轴的匀强电场(图中未画出).一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进入第Ⅳ象限,然后做圆周运动,从Q点垂直于x轴进入第Ⅰ象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,可以求出的物理量有( )
如图所示,直角坐标系xOy位于竖直平面内,y轴竖直向上.第Ⅲ、Ⅳ象限内有垂直于坐标面向外的匀强磁场,第Ⅳ象限同时存在方向平行于y轴的匀强电场(图中未画出).一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进入第Ⅳ象限,然后做圆周运动,从Q点垂直于x轴进入第Ⅰ象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,可以求出的物理量有( )
 如图所示,直角坐标系xOy位于竖直平面内,y轴竖直向上.第Ⅲ、Ⅳ象限内有垂直于坐标面向外的匀强磁场,第Ⅳ象限同时存在方向平行于y轴的匀强电场(图中未画出).一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进入第Ⅳ象限,然后做圆周运动,从Q点垂直于x轴进入第Ⅰ象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,可以求出的物理量有( )
如图所示,直角坐标系xOy位于竖直平面内,y轴竖直向上.第Ⅲ、Ⅳ象限内有垂直于坐标面向外的匀强磁场,第Ⅳ象限同时存在方向平行于y轴的匀强电场(图中未画出).一带电小球从x轴上的A点由静止释放,恰好从P点垂直于y轴进入第Ⅳ象限,然后做圆周运动,从Q点垂直于x轴进入第Ⅰ象限,Q点距O点的距离为d,重力加速度为g.根据以上信息,可以求出的物理量有( )| A. | 圆周运动的速度大小 | B. | 电场强度的大小和方向 | ||
| C. | 小球在第Ⅳ象限运动的时间 | D. | 磁感应强度大小 |
1.下列说法正确的是( )
| A. | 卢瑟福通过α粒子散射实验建立了原子核式结构模型 | |
| B. | 对于任何一种金属都存在一个“最小波长”,入射光的波长必须大于这个波长,才能产生光电效应 | |
| C. | 放射性元素的半衰期与核内自身因素有关,与原子所处的化学状态和外部条件也有关 | |
| D. | 爱因斯坦在对光电效应的研究中,提出了光子说 |
 如图所示,在竖直平面内,由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的组合轨道,AB与CD光滑,BC轨道粗糙,动摩擦因数μ=0.1,AB与BC的连接处是半径很小的圆弧,BC与CD相切,圆形轨道CD的半径为R=2m.质量为m=1kg的小物块从倾斜轨道上距水平面高为h=10m处由静止开始下滑,恰好通过圆弧形的最高点D(g=10m/s2)求:
如图所示,在竖直平面内,由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的组合轨道,AB与CD光滑,BC轨道粗糙,动摩擦因数μ=0.1,AB与BC的连接处是半径很小的圆弧,BC与CD相切,圆形轨道CD的半径为R=2m.质量为m=1kg的小物块从倾斜轨道上距水平面高为h=10m处由静止开始下滑,恰好通过圆弧形的最高点D(g=10m/s2)求: 如图(a)所示,倾角为45°、高为h的斜面固定在水平地面上,小球从高为H(2h>H>h)的某处自由下落,与斜面碰撞(不计能量损失)后做平抛运动.
如图(a)所示,倾角为45°、高为h的斜面固定在水平地面上,小球从高为H(2h>H>h)的某处自由下落,与斜面碰撞(不计能量损失)后做平抛运动. 如图所示,一根长直棒AB竖直地插入水平池底,水深a=0.8m,棒露出水面部分的长度b=0.6m,太阳光斜射到水面上,与水面夹角α=37°,已知水的折射率n=$\frac{4}{3}$,sin37°=0.6,cos37°=0.8.求:
如图所示,一根长直棒AB竖直地插入水平池底,水深a=0.8m,棒露出水面部分的长度b=0.6m,太阳光斜射到水面上,与水面夹角α=37°,已知水的折射率n=$\frac{4}{3}$,sin37°=0.6,cos37°=0.8.求:
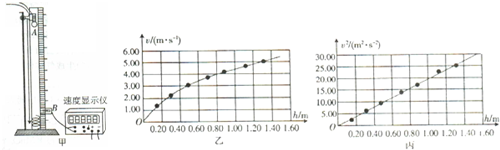
 如图所示,将打点计时器固定在铁架台上,让重物带动纸带从静止开始自由下落,利用此装置可测定重力加速度.
如图所示,将打点计时器固定在铁架台上,让重物带动纸带从静止开始自由下落,利用此装置可测定重力加速度.