题目内容
18. 如图所示,两个劲度系数分别为k 1和k 2的轻质弹簧竖直悬挂,弹簧下端用光滑细绳连接,并有一光滑的轻滑轮放在细绳上.当滑轮下端挂一重为G的物体时,滑轮下滑一段距离,则下列结论正确的有( )
如图所示,两个劲度系数分别为k 1和k 2的轻质弹簧竖直悬挂,弹簧下端用光滑细绳连接,并有一光滑的轻滑轮放在细绳上.当滑轮下端挂一重为G的物体时,滑轮下滑一段距离,则下列结论正确的有( )| A. | 两弹簧的伸长量相等 | |
| B. | 两弹簧的弹力不一定相等 | |
| C. | 重物下降的距离为 $\frac{G}{{k}_{1}+{k}_{2}}$ | |
| D. | 重物下降的距离为$\frac{G({k}_{1}+{k}_{2})}{4{k}_{1}{k}_{2}}$ |
分析 对滑轮进行受力分析,应用平衡条件可求得弹簧的弹力,重物下降的距离就是两根弹簧伸长的量除以2.
解答 解:A、对滑轮受力分析如图:
因为F1、F2是同一根绳上的力,故大小相等,即:F1=F2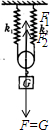
由平衡条件得:F1+F2=G
解得:F1=$\frac{G}{2}$,
根据胡克定律得,${x}_{1}=\frac{{F}_{1}}{{k}_{1}}=\frac{G}{2{k}_{1}}$,${x}_{2}=\frac{{F}_{2}}{{k}_{2}}=\frac{G}{2{k}_{2}}$,由于劲度系数不一定相同,则伸长量不一定相等,故A、B错误.
C、两弹簧的伸长量之和x=${x}_{1}+{x}_{2}=\frac{G}{2{k}_{1}}+\frac{G}{2{k}_{2}}$=$\frac{G({k}_{1}+{k}_{2})}{2{k}_{1}{k}_{2}}$,则重物下降的距离h=$\frac{x}{2}$=$\frac{G({k}_{1}+{k}_{2})}{4{k}_{1}{k}_{2}}$,故C错误,D正确.
故选:D.
点评 本题为受力平衡的简单应用,受力分析后应用平衡条件求解即可;注意应用动滑轮的基本原理.

练习册系列答案
相关题目
1.假如一做圆周运动的人造地球卫星的轨道半径增大到原来的2倍仍做圆周运动,则( )
| A. | 根据公式v=ωr,可知卫星运动的线速度增大到原来2倍 | |
| B. | 根据公式a=ω2r,可知卫星运动的加速度读增大到原来2倍 | |
| C. | 根据公式F=m$\frac{{v}^{2}}{r}$,可知卫星所需的向心力将减小到原来的$\frac{1}{2}$ | |
| D. | 根据公式F=$\frac{GMm}{{r}^{2}}$,可知地球提供的向心力将减小到原来的$\frac{1}{4}$ |
6. a、b、c是三个电荷量相同、质量不同的带电粒子,以相同的初速度由同一点垂直场强方向进入偏转电场,仅在电场力的作用下,运动轨迹如图所示,其中b恰好沿着极板边缘飞出电场.粒子a、b、c在电场中运动的过程中,下列说法正确的是( )
a、b、c是三个电荷量相同、质量不同的带电粒子,以相同的初速度由同一点垂直场强方向进入偏转电场,仅在电场力的作用下,运动轨迹如图所示,其中b恰好沿着极板边缘飞出电场.粒子a、b、c在电场中运动的过程中,下列说法正确的是( )
 a、b、c是三个电荷量相同、质量不同的带电粒子,以相同的初速度由同一点垂直场强方向进入偏转电场,仅在电场力的作用下,运动轨迹如图所示,其中b恰好沿着极板边缘飞出电场.粒子a、b、c在电场中运动的过程中,下列说法正确的是( )
a、b、c是三个电荷量相同、质量不同的带电粒子,以相同的初速度由同一点垂直场强方向进入偏转电场,仅在电场力的作用下,运动轨迹如图所示,其中b恰好沿着极板边缘飞出电场.粒子a、b、c在电场中运动的过程中,下列说法正确的是( )| A. | a、b运动的时间相同 | |
| B. | a的质量最大,c的质量最小 | |
| C. | 动量的增量相比,a的最小,b和c的一样大 | |
| D. | 动能的增量相比,c的最大,a和b的一样大 |
13.现用某一光电管进行光电效应实验,当用某一频率的光入射时,有光电流产生.下列说法正确的是( )
| A. | 保持入射光的频率不变,入射光的光强变大,饱和光电流变大 | |
| B. | 入射光的频率变高,饱和光电流变大 | |
| C. | 保持入射光的光强不变,不断减小入射光的频率,始终有光电流产生 | |
| D. | 遏止电压的大小与入射光的频率有关,与入射光的光强无关 |
3.下列说法中正确的是( )
| A. | 放射性元素的半衰期随温度的升高而变短 | |
| B. | β射线是原子被电离后核外电子形成的电子流 | |
| C. | 同种元素的两种同位素具有相同的核子数 | |
| D. | 链式反应中,重核裂变时放出的可以使裂变不断进行下去的粒子是中子 |
7. 一水平轻质弹簧左端固定在墙上,用大小为F1的力水平向右拉弹簧(如图甲),弹簧的伸长量为x1;用大小为F2的力水平向左压弹簧(如图乙),弹簧的压缩量为x2.若上述两种情况弹簧均处于弹性限度内,且最终静止.下列判断正确的是( )
一水平轻质弹簧左端固定在墙上,用大小为F1的力水平向右拉弹簧(如图甲),弹簧的伸长量为x1;用大小为F2的力水平向左压弹簧(如图乙),弹簧的压缩量为x2.若上述两种情况弹簧均处于弹性限度内,且最终静止.下列判断正确的是( )
 一水平轻质弹簧左端固定在墙上,用大小为F1的力水平向右拉弹簧(如图甲),弹簧的伸长量为x1;用大小为F2的力水平向左压弹簧(如图乙),弹簧的压缩量为x2.若上述两种情况弹簧均处于弹性限度内,且最终静止.下列判断正确的是( )
一水平轻质弹簧左端固定在墙上,用大小为F1的力水平向右拉弹簧(如图甲),弹簧的伸长量为x1;用大小为F2的力水平向左压弹簧(如图乙),弹簧的压缩量为x2.若上述两种情况弹簧均处于弹性限度内,且最终静止.下列判断正确的是( )| A. | 若F1>F2,则x1>x2 | |
| B. | 若F1<F2,则x1>x2 | |
| C. | 无论F1、F2大小关系如何,都有x1=x2 | |
| D. | 无论F1、F2大小关系如何,都有x1≠x2 |
 如图所示,摩托车做特技表演时,由静止开始加速冲向高台,高台的末端部分是直径为h的一小段圆弧,摩托车从高台末端以速度v1水平飞出.若摩托车冲向高台的过程中保持额定功率P行驶,冲到高台上所用时间为t,人和车的总质量为m,台高为h.不计空气阻力.求:
如图所示,摩托车做特技表演时,由静止开始加速冲向高台,高台的末端部分是直径为h的一小段圆弧,摩托车从高台末端以速度v1水平飞出.若摩托车冲向高台的过程中保持额定功率P行驶,冲到高台上所用时间为t,人和车的总质量为m,台高为h.不计空气阻力.求: