题目内容
2.估算地球的质量和密度,已知地球的半径R,自转周期T,万有引力恒量G,及以下条件之一:(1)地球表面的重力加速度g;
(2)环绕地球表面作圆周运动的卫星的周期T1;
(3)绕地球做圆周运动的卫星的高度为h,周期T2;
(4)绕地球做圆周运动的卫星的高度为h,速度为v.
分析 根据旋转天体绕中心天体运行的模型,由旋转天体公转半径和周期求出中心天体的质量分析:
由卫星绕地球运行的周期T和轨道板,能求出地球的质量.
根据万有引力等于重力求出地球的质量
根据密度公式求解.
解答 解:(1)根据万有引力等于重力有
$\frac{GMm}{{R}^{2}}$=mg
M=$\frac{{gR}^{2}}{G}$,
ρ=$\frac{M}{\frac{4{πR}^{3}}{3}}$=$\frac{3g}{4πGR}$,
(2)根据万有引力提供圆周运动向心力有
$\frac{GMm}{{r}^{2}}$m$\frac{{4π}^{2}}{{T}^{2}}$r,r=R
环绕地球表面作圆周运动的卫星的周期T1;
M=$\frac{{{4π}^{2}R}^{3}}{{GT}_{1}^{2}}$,
ρ=$\frac{M}{\frac{4{πR}^{3}}{3}}$=$\frac{3π}{{GT}_{1}^{2}}$,
(3)根据万有引力提供圆周运动向心力有
$\frac{GMm}{{r}^{2}}$m$\frac{{4π}^{2}}{{T}^{2}}$r,r=h+R
绕地球做圆周运动的卫星的高度为h,周期T2;
M=$\frac{{{4π}^{2}(R+h)}^{3}}{{GT}_{2}^{2}}$,
ρ=$\frac{M}{\frac{4{πR}^{3}}{3}}$=$\frac{3{π(R+h)}^{3}}{{{GR}^{3}T}_{2}^{2}}$
(4)根据万有引力提供圆周运动向心力有
$\frac{GMm}{{r}^{2}}$m$\frac{{v}^{2}}{r}$,r=h+R
绕地球做圆周运动的卫星的高度为h,速度为v.
M=$\frac{{(R+h)v}^{2}}{G}$
ρ=$\frac{M}{\frac{4{πR}^{3}}{3}}$=$\frac{{3(R+h)v}^{2}}{4π{GR}^{3}}$
答:(1)地球表面的重力加速度g,地球的质量和密度分别是$\frac{{gR}^{2}}{G}$和$\frac{3g}{4πGR}$;
(2)环绕地球表面作圆周运动的卫星的周期T1,地球的质量和密度分别是$\frac{{{4π}^{2}R}^{3}}{{GT}_{1}^{2}}$和$\frac{3π}{{GT}_{1}^{2}}$;
(3)绕地球做圆周运动的卫星的高度为h,周期T2,地球的质量和密度分别是$\frac{{{4π}^{2}(R+h)}^{3}}{{GT}_{2}^{2}}$和$\frac{3{π(R+h)}^{3}}{{{GR}^{3}T}_{2}^{2}}$;
(4)绕地球做圆周运动的卫星的高度为h,速度为v,地球的质量和密度分别是$\frac{{(R+h)v}^{2}}{G}$和$\frac{{3(R+h)v}^{2}}{4π{GR}^{3}}$.
点评 计算中心天体质量的方法主要有:地球表面重力与万有引力相等,万有引力提供环绕天体的向心力,据此列式分析即可,关键是掌握方法.


| A. | 沿AB方向磁场在迅速减小 | B. | 沿AB方向磁场在迅速增加 | ||
| C. | 沿BA方向磁场在迅速增加 | D. | 沿BA方向磁场在迅速减弱 |
| A. | 4.0×105J | B. | 2.0×105J | C. | 2.0×104J | D. | 1.0×104J |
 如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC是水平的,其长度d=0.60m.盆边缘的高度为h=0.30m.在A处放一个质量为m的小物块并让其从静止下滑.已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数为μ=0.10.小物块在盆内来回滑动,最后停下来,则停的地点到B的距离为( )
如图所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,BC是水平的,其长度d=0.60m.盆边缘的高度为h=0.30m.在A处放一个质量为m的小物块并让其从静止下滑.已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数为μ=0.10.小物块在盆内来回滑动,最后停下来,则停的地点到B的距离为( )| A. | 0.50 m | B. | 0.60 m | C. | 0.10 m | D. | 0 |
| A. | 小球上升的过程中重力做功的平均功率大于下降的过程中重力做功的平均功率 | |
| B. | 小球上升和下降的整个过程中机械能减少了fH | |
| C. | 小球上升的过程中重力势能增加了mgH | |
| D. | 小球上升的过程中动能减少了mgH |
| A. | 300km/h | B. | 260km/h | C. | 150km/h | D. | 173km/h |
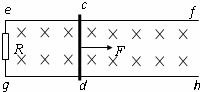 如图,ef,gh为水平放置的足够长的平行光滑导轨,导轨间距为L=1m,导轨左端连接一个R=2Ω的电阻,将一根质量为0.2kg的金属棒cd垂直地放置导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直于导轨平面向下.现对金属棒施加一水平向右的拉力F,且保持拉力的功率恒为P=18W,使棒从静止开始向右运动.
如图,ef,gh为水平放置的足够长的平行光滑导轨,导轨间距为L=1m,导轨左端连接一个R=2Ω的电阻,将一根质量为0.2kg的金属棒cd垂直地放置导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直于导轨平面向下.现对金属棒施加一水平向右的拉力F,且保持拉力的功率恒为P=18W,使棒从静止开始向右运动. 如图所示,质量为m2=0.6kg的薄木板静止在光滑水平地面上,木板上有一质量为m1=0.2kg的小铁块,它离木板的右端距离d=0.5m,铁块与木块间的动摩擦因数为0.2,现用拉力向左以3m/s2的加速度将木板从铁块下抽出,则:
如图所示,质量为m2=0.6kg的薄木板静止在光滑水平地面上,木板上有一质量为m1=0.2kg的小铁块,它离木板的右端距离d=0.5m,铁块与木块间的动摩擦因数为0.2,现用拉力向左以3m/s2的加速度将木板从铁块下抽出,则: