题目内容
7.若“天宫1号”宇宙飞船的质量为m,距离地面的高度h=R(其中R为地球半径).假设飞船绕地球做匀速圆周运动,地球表面处的重力加速度为g,引力常量为G,则“天宫1号”飞船运动的加速度大小为$\frac{g}{4}$,旋转周期为4π$\sqrt{\frac{2R}{g}}$.分析 在地球表面,忽略地球自传的情况下,重力等于万有引力,列式求解重力加速度表达式;在距离地面的高度h=R的轨道上,飞船绕地球做匀速圆周运动,万有引力等于向心力,根据牛顿第二定律列式;最后联立求解即可.
解答 解:在地球表面,忽略地球自传的情况下,重力等于万有引力,故:
$mg=G\frac{Mm}{R^2}$
在距离地面的高度h=R的轨道上,飞船绕地球做匀速圆周运动,根据牛顿第二定律,有:
$G\frac{Mm}{{{{(h+R)}^2}}}=ma$
$G\frac{Mm}{{{{(h+R)}^2}}}=m\frac{{4{π^2}}}{T^2}(R+h)$
联立解得:
a=$\frac{g}{4}$
T=4π$\sqrt{\frac{2R}{g}}$
故答案为:$\frac{g}{4}$,4π$\sqrt{\frac{2R}{g}}$.
点评 本题关键是明确卫星的动力学原理为万有引力等于向心力,同时要会求解重力加速度的表达式,基础题目.

练习册系列答案
相关题目
17. 如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )
如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )
 如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )
如图所示,在空间直角坐标系Oxyz中存在有沿x轴正方向的匀强磁场,在直角坐标系中选取如图所示的abc-a′b′c′棱柱形空间.通过面积S1(abb′a′所围的面积)、S2(acc′a′所围的面积)和S3(cbb′c′所围的面积)的磁通量分别为Φ1、Φ2和Φ3,则( )| A. | Φ1=Φ2 | B. | Φ1>Φ2 | C. | Φ1>Φ3 | D. | Φ3>Φ2 |
18.质量为1kg的物体,以2m/s的速度在光滑水平长直轨道上滑行.从某时刻起对该物体施加一个沿轨道的水平力,经过一段时间后,物体的速度变化量大小为4m/s,则在此过程中水平力做的功可能为( )
| A. | 0 | B. | 2J | C. | 8J | D. | 16J |
15.下表是某同学做“探究弹力大小和弹簧的伸长的关系”实验所测量的几组数据:
请你把6组对应的点标在坐标纸中,根据这些数据点作出F-L图线,由此图线可以得出该弹簧的自然长度L0=5.0cm,劲度系数k=10N/m(计算结果保留两位有效数字).

| 弹簧长度L(cm) | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 35.0 | 40.0 |
| 弹簧弹力F(N) | 0 | 0.5 | 1.0 | 1.4 | 2.0 | 2.6 | 3.0 | 3.5 |

2.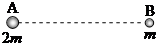 相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
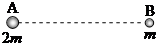 相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )
相距为d、质量分别为2m和m的两颗恒星A和B组成双星系统,在万有引力作用下各自绕它们连线上的某一固定点,在同一平面内做匀速圆周运动.设两颗恒星的转动半径分别为RA、RB,速度大小分别为vA、vB,动能分别为EkA、EkB,引力常量为G,则下列关系中正确的是( )| A. | RA=2RB | B. | vA=2vB | C. | EkA=EkB | D. | EkA+EkB=$\frac{G{m}^{2}}{d}$ |
19. 如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )
如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )
 如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )
如图电路中,电源的电动势E和内阻r均为定值,R1R2为滑动变阻器,R0为定值电阻.当变阻器的阻值发生变化时,以下推断正确的是( )| A. | 若只增大R1,则R0消耗的功率一定减小 | |
| B. | 若只增大R2,则R1消耗的功率一定变小 | |
| C. | 若只减小R1,则R1消耗的功率一定变小 | |
| D. | 若只减小R2,则电源的输出功率一定变小 |
16.关于平行板电容器的电容,下列说法正确的是( )
| A. | 电容器带的电荷量越多,电容就越大 | |
| B. | 电容器的电容等于电容器所带的电荷量与两极板间的电压的比值 | |
| C. | 电容器的电容与电容器所带的电荷量成正比,与两极板间的电压成反比 | |
| D. | 电容器的电容由电容器自身结构决定,与两极板间的电压无关 |
 如图所示,半径为R=1.5m的光滑圆弧支架竖直放置,圆心角θ=60°,支架的底部CD离地面足够高,圆心O在C点的正上方,右侧边缘P点固定一个光滑小轮,可视为质点的小球A、B分别系在足够长的跨过小轮的轻绳两端,两球的质量分别为mA=0.3kg、mB=0.1kg.将A球从紧靠小轮处由静止释放,求:
如图所示,半径为R=1.5m的光滑圆弧支架竖直放置,圆心角θ=60°,支架的底部CD离地面足够高,圆心O在C点的正上方,右侧边缘P点固定一个光滑小轮,可视为质点的小球A、B分别系在足够长的跨过小轮的轻绳两端,两球的质量分别为mA=0.3kg、mB=0.1kg.将A球从紧靠小轮处由静止释放,求: