题目内容
18. 如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的单匝正方形导线框架EFGH正好与上述磁场区域的边界重合,导线框的电阻为R.现使导线框以周期T绕其中心O点在纸面内匀速转动,经过$\frac{T}{8}$导线框转到图中虚线位置,则在这$\frac{T}{8}$时间内( )
如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的单匝正方形导线框架EFGH正好与上述磁场区域的边界重合,导线框的电阻为R.现使导线框以周期T绕其中心O点在纸面内匀速转动,经过$\frac{T}{8}$导线框转到图中虚线位置,则在这$\frac{T}{8}$时间内( )| A. | 顺时针方向转动时,感应电流方向为E→F→G→H→E | |
| B. | 平均感应电动势大小等于$\frac{8(3-2\sqrt{2}){a}^{2}B}{T}$ | |
| C. | 平均感应电动势大小等于$\frac{16{a}^{2}B}{9T}$ | |
| D. | 通过导线框横截面的电荷量为$\frac{(3-2\sqrt{2}){a}^{2}B}{R}$ |
分析 根据楞次定律判断感应电流的方向.
运用法拉第电磁感应定律求出平均感应电动势大小.
根据电量的表达式求出通过导线框横截面的电荷量.
解答 解:A、由于虚线位置是经过$\frac{T}{8}$到达的,而且线框是顺时针方向转动,所以线框的磁通量是变小的.
根据楞次定律,感应电流产生的磁场跟原磁场方向相同,即感应电流产生的磁场方向为垂直纸面向外,根据右手定则,我们可以判断出感应电流的方向为:E→H→G→F→E,故A错误.
B、根据法拉第电磁感应定律得:平均感应电动势E=$\frac{△Φ}{△t}$=$\frac{B△S}{△t}$, 由几何知识得:OC=$\frac{\sqrt{2}}{2}$a,0A=$\frac{1}{2}$a,AB=AC,
由几何知识得:OC=$\frac{\sqrt{2}}{2}$a,0A=$\frac{1}{2}$a,AB=AC,
根据几何关系找出有磁场穿过面积的变化△s=(3-2$\sqrt{2}$)a2,解得:$\overline{E}$=$\frac{8(3-2\sqrt{2}){a}^{2}B}{T}$,故B正确,故C错误.
D、通过导线框横截面的电荷量q=$\overline{I}$•△t=$\frac{\overline{E}}{R}$•△t=$\frac{(3-2\sqrt{2}){a}^{2}B}{R}$,故D正确.
故选:BD.
点评 分析清楚线框的运动过程、知道磁通量如何变化、求出磁通量的变化量是解题的前提与关键;要掌握应用楞次定律判断感应电流方向的方法与步骤;应用楞次定律、法拉第电磁感应定律、欧姆定律与电流的定义式可以解题.

练习册系列答案
相关题目
15.关于静电的利用和防范,以下说法中正确的是( )
| A. | 静电复印是防范静电的 | |
| B. | 为了防止静电积聚,飞机起落架的轮胎必须用绝缘橡胶制成 | |
| C. | 油罐车行驶途中车尾有一条铁链拖在地上,可以避免产生电火花引起的爆炸 | |
| D. | 静电植绒是利用异种电荷相互吸引而使绒毛吸附在底料上 |
13. 如图,固定在水平桌面上的光滑金属导轨cd、eg处于方向竖直向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点d、e之间连接一电阻,其它部分电阻忽略不计.现用一水平向右的恒力F作用在金属杆ab上,使金属杆由静止开始向右沿导轨滑动,滑动中杆ab始终垂直于导轨.金属杆受到的安培力用F安表示,则下列说法正确的是( )
如图,固定在水平桌面上的光滑金属导轨cd、eg处于方向竖直向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点d、e之间连接一电阻,其它部分电阻忽略不计.现用一水平向右的恒力F作用在金属杆ab上,使金属杆由静止开始向右沿导轨滑动,滑动中杆ab始终垂直于导轨.金属杆受到的安培力用F安表示,则下列说法正确的是( )
 如图,固定在水平桌面上的光滑金属导轨cd、eg处于方向竖直向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点d、e之间连接一电阻,其它部分电阻忽略不计.现用一水平向右的恒力F作用在金属杆ab上,使金属杆由静止开始向右沿导轨滑动,滑动中杆ab始终垂直于导轨.金属杆受到的安培力用F安表示,则下列说法正确的是( )
如图,固定在水平桌面上的光滑金属导轨cd、eg处于方向竖直向下的匀强磁场中,金属杆ab与导轨接触良好.在两根导轨的端点d、e之间连接一电阻,其它部分电阻忽略不计.现用一水平向右的恒力F作用在金属杆ab上,使金属杆由静止开始向右沿导轨滑动,滑动中杆ab始终垂直于导轨.金属杆受到的安培力用F安表示,则下列说法正确的是( )| A. | 金属杆ab做匀加速直线运动 | |
| B. | 金属杆ab运动过程中回路中有顺时针方向的电流 | |
| C. | 金属杆ab所受到的F安先不断增大,后保持不变 | |
| D. | 金属杆ab克服安培力做功的功率与时间的平方成正比 |
8.下列关于电场的叙述中正确的是( )
| A. | 以点电荷为圆心,r为半径的球面上,各点的场强都相同 | |
| B. | 正电荷周围的场强一定比负电荷周围的场强大 | |
| C. | 电场中某点的试探电荷电荷量变为原来两倍,该试探电荷所受电场力不变 | |
| D. | 电荷在电场中某点所受电场力的方向与该点电场的方向可能相反 |
 如图所示,MN、PQ为足够长的平行导轨,间距L=0.5m.导轨平面与水平面间的夹角θ=37°.NQ⊥MN,NQ间连接有一个R=3Ω的电阻.有一匀强磁场垂直于导轨平面,磁感应强度为B=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,金属棒的电阻r=2Ω,其余部分电阻不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时速度大小开始保持不变,cd 距离NQ为s=2m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,MN、PQ为足够长的平行导轨,间距L=0.5m.导轨平面与水平面间的夹角θ=37°.NQ⊥MN,NQ间连接有一个R=3Ω的电阻.有一匀强磁场垂直于导轨平面,磁感应强度为B=1T.将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,金属棒的电阻r=2Ω,其余部分电阻不计.现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行.已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时速度大小开始保持不变,cd 距离NQ为s=2m.试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)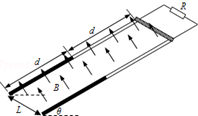 如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为L=0.2m,长为2d,d=0.5m,上半段d导轨光滑,下半段d导轨的动摩擦因素为μ=$\frac{\sqrt{3}}{6}$,导轨平面与水平面的夹角为θ=30°.匀强磁场的磁感应强度大小为B=5T,方向与导轨平面垂直.质量为m=0.2kg的导体棒从导轨的顶端由静止释放,在粗糙的下半段一直做匀速运,导体棒始终与导轨垂直,接在两导轨间的电阻为R=3Ω,导体棒的电阻为r=1Ω,其他部分的电阻均不计,重力加速度取g=10m/s2,求:
如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为L=0.2m,长为2d,d=0.5m,上半段d导轨光滑,下半段d导轨的动摩擦因素为μ=$\frac{\sqrt{3}}{6}$,导轨平面与水平面的夹角为θ=30°.匀强磁场的磁感应强度大小为B=5T,方向与导轨平面垂直.质量为m=0.2kg的导体棒从导轨的顶端由静止释放,在粗糙的下半段一直做匀速运,导体棒始终与导轨垂直,接在两导轨间的电阻为R=3Ω,导体棒的电阻为r=1Ω,其他部分的电阻均不计,重力加速度取g=10m/s2,求: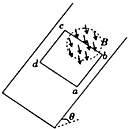 如图所示,粗糙斜面的倾角θ=37°,斜面上半径r=0.5m的圆形区域内存在着垂直于斜面向下的匀强磁场,一刚性单匝正方形线框abcd的bc边与斜面底端平行且恰好过圆形区域的一条直径.已知线框的质量m=0.2kg、电阻R=0.25Ω、边长L=1.2m,与斜面间的动摩擦因数μ=0.5,从t=0时刻起,磁场的磁感应强度按B=2-$\frac{2}{π}$t(T)的规律变化,开始时线框静止在斜面上,设最大静摩擦力等于滑动摩擦力,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,粗糙斜面的倾角θ=37°,斜面上半径r=0.5m的圆形区域内存在着垂直于斜面向下的匀强磁场,一刚性单匝正方形线框abcd的bc边与斜面底端平行且恰好过圆形区域的一条直径.已知线框的质量m=0.2kg、电阻R=0.25Ω、边长L=1.2m,与斜面间的动摩擦因数μ=0.5,从t=0时刻起,磁场的磁感应强度按B=2-$\frac{2}{π}$t(T)的规律变化,开始时线框静止在斜面上,设最大静摩擦力等于滑动摩擦力,g取10m/s2,sin37°=0.6,cos37°=0.8,求:
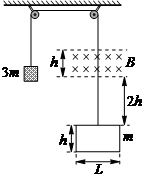 如图所示,质量为3m的重物与一质量为m的线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知线框电阻为R,横边边长为L,水平方向匀强磁场的磁感应强度为B,磁场上下边界的距离、线框竖直边长均为h.初始时刻,磁场的下边缘和线框上边缘的高度差为2h,将重物从静止开始释放,线框穿出磁场前,若线框已经做匀速直线运动,滑轮质量、摩擦阻力均不计.求:
如图所示,质量为3m的重物与一质量为m的线框用一根绝缘细线连接起来,挂在两个高度相同的定滑轮上,已知线框电阻为R,横边边长为L,水平方向匀强磁场的磁感应强度为B,磁场上下边界的距离、线框竖直边长均为h.初始时刻,磁场的下边缘和线框上边缘的高度差为2h,将重物从静止开始释放,线框穿出磁场前,若线框已经做匀速直线运动,滑轮质量、摩擦阻力均不计.求: