题目内容
14.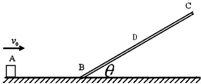 如图,BC为长度一定可以绕B点转动调节倾角大小的斜面,AB为水平面,刚开始时,斜面倾角为45°,一可视为质点的小滑块从A点出发向左运动冲上斜面,初速度大小为v0,恰好能到达斜面中点D,已知物块与斜面和水平面的滑动摩擦因素均为μ=1,不计物块由水平面进入斜面瞬间的能量损失,下列说法正确的是( )
如图,BC为长度一定可以绕B点转动调节倾角大小的斜面,AB为水平面,刚开始时,斜面倾角为45°,一可视为质点的小滑块从A点出发向左运动冲上斜面,初速度大小为v0,恰好能到达斜面中点D,已知物块与斜面和水平面的滑动摩擦因素均为μ=1,不计物块由水平面进入斜面瞬间的能量损失,下列说法正确的是( )| A. | 保持初速v0不变,逐渐减小斜面倾角,小球不可能到达C点 | |
| B. | 保持初速v0不变,逐渐减小斜面倾角,每次小滑块克服摩擦阻力做的功相等 | |
| C. | 保持斜面倾角不变,初速度变为2v0,小滑块一定能冲过C点 | |
| D. | 保持倾角和初速度不变,滑动摩擦因素μ=0.5时,小滑块一定能冲过C点 |
分析 对ABD过程和ABDC过程分别应用动能定理求解.
解答 解:由题意知 2sBD=SBC
A、对ABD过程应用动能定理,得
-μmgsAB-mgsBDsin θ-μmgsBDcos θ=0-$\frac{1}{2}$mv${\;}_{0}^{2}$
又u=1 得mgsAB+mgsBDsin θ+mgsBDcos θ=$\frac{1}{2}$mv${\;}_{0}^{2}$
mgsAB+$\sqrt{2}$mgsBDsin(θ+45°)=$\frac{1}{2}$mv${\;}_{0}^{2}$
$\sqrt{2}$mgsBDsin(θ+45°)<2$\sqrt{2}$mgsBDsinθ 故A正确
B、保持初速v0不变,逐渐减小斜面倾角,重力做功减小,摩擦力做功增大,故B错误
C、对ABDC过程应用动能定理,得-μmgsAB-mg×2sBDsin θ-μmg×2sBDcos θ=0-$\frac{1}{2}$mv2 $\frac{1}{2}$m×4v${\;}_{0}^{2}$
解得 $\frac{1}{2}$mv2<$\frac{1}{2}$m×4v${\;}_{0}^{2}$,故C正确
D、保持倾角和初速度不变,滑动摩擦因素μ=0.5时,对ABD过程和ABDC过程分别应用动能定理,解得
小滑块刚好到达C点,故D错误
故选:AC
点评 本题考查动能定理及牛顿第二定律的应用等,要注意正确受力分析及过程分析,再根据需要选择合适的物理规律求解即可

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
19.一质点在外力作用下由静止开始作直线运动,其v-t图象如图所示,该质点( )


| A. | 在0~1s内做加速度增大的加速运动 | B. | 在第1s末速度方向发生了变化 | ||
| C. | 在t=1.5s时离出发点最远 | D. | 在1.5~2.5s内做匀减速直线运动 |
9. 如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )
如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )
 如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )
如图所示,两个固定的相同细圆环相距一定的距离,同轴平行放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷,一带正电的粒子从很远处沿轴线飞来并穿过两环,则( )| A. | 带电粒子在O1和O2点加速大小相等,方向向反 | |
| B. | 带电粒子从O1运动到O2,电势能一直增加 | |
| C. | 带电粒子在O1和O2连线中点动能最小 | |
| D. | 轴线上O1点右侧,O2点左侧都存在场强为零的点,它们关于O1、O2连线中点对称 |
19. 如图所示,电路中的A、B是两个完全相同的灯泡,L是一个自感系数很大、电阻可忽略的自感线圈,C是电容很大的电容器.当开关S断开与闭合时,关于A、B两灯泡发光情况说法正确的是( )
如图所示,电路中的A、B是两个完全相同的灯泡,L是一个自感系数很大、电阻可忽略的自感线圈,C是电容很大的电容器.当开关S断开与闭合时,关于A、B两灯泡发光情况说法正确的是( )
 如图所示,电路中的A、B是两个完全相同的灯泡,L是一个自感系数很大、电阻可忽略的自感线圈,C是电容很大的电容器.当开关S断开与闭合时,关于A、B两灯泡发光情况说法正确的是( )
如图所示,电路中的A、B是两个完全相同的灯泡,L是一个自感系数很大、电阻可忽略的自感线圈,C是电容很大的电容器.当开关S断开与闭合时,关于A、B两灯泡发光情况说法正确的是( )| A. | S刚闭合后,B灯亮一下又逐渐变暗,A灯逐渐变亮 | |
| B. | S刚闭合后,A灯亮一下又逐渐变暗,B灯逐渐变亮 | |
| C. | S闭合足够长时间后,A灯泡和B灯泡一样亮 | |
| D. | S闭合足够长时间后再断开,B灯立即熄灭,A灯逐渐熄灭 |
3. 如图所示,在一均匀弹性介质中沿一水平直线(平衡位置)标注多个质点Sabcdefgh,相邻两点间的距离为1m,t=0时刻,波源S作简谐振动,起始速度方向竖直向上,振动由此以1m/s的速度开始向右传播,从而形成简谐横波.t=1.0s时,波源S第一次到达波峰处,由此可以判断,下列说法正确的是( )
如图所示,在一均匀弹性介质中沿一水平直线(平衡位置)标注多个质点Sabcdefgh,相邻两点间的距离为1m,t=0时刻,波源S作简谐振动,起始速度方向竖直向上,振动由此以1m/s的速度开始向右传播,从而形成简谐横波.t=1.0s时,波源S第一次到达波峰处,由此可以判断,下列说法正确的是( )
 如图所示,在一均匀弹性介质中沿一水平直线(平衡位置)标注多个质点Sabcdefgh,相邻两点间的距离为1m,t=0时刻,波源S作简谐振动,起始速度方向竖直向上,振动由此以1m/s的速度开始向右传播,从而形成简谐横波.t=1.0s时,波源S第一次到达波峰处,由此可以判断,下列说法正确的是( )
如图所示,在一均匀弹性介质中沿一水平直线(平衡位置)标注多个质点Sabcdefgh,相邻两点间的距离为1m,t=0时刻,波源S作简谐振动,起始速度方向竖直向上,振动由此以1m/s的速度开始向右传播,从而形成简谐横波.t=1.0s时,波源S第一次到达波峰处,由此可以判断,下列说法正确的是( )| A. | 该横波的周期为4.0s | |
| B. | 质点b和质点d在起振后的振动步调始终一致 | |
| C. | 在t=4.0s时质点c有最大加速 | |
| D. | 在t=7.0s时质点e速度最大,且方向向左 | |
| E. | 在t=10.0s时质点c、g正好到达波谷 |
4.最早发现静止点电荷间相互作用规律的科学家是( )
| A. | 安培 | B. | 法拉第 | C. | 麦克斯韦 | D. | 库仑 |
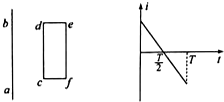 通电直导线周围的某点磁感应强度B的大小与该点到直导线的距离成反比,与通电直导线中的电流的大小成正比,可以用公式B=k$\frac{I}{r}$来表示,其中k为比例常数,俯视图如图所示,在光滑水平面上有一通电直导线ab,旁边有一矩形金属线框cdef,cd边与导线ab平行,当导线ab中通如图所示电流时(设a流向b为电流的正方向),为使矩形金属线框cdef静止不动,需加一水平方向的力F(设向右为正方向),则正确的是( )
通电直导线周围的某点磁感应强度B的大小与该点到直导线的距离成反比,与通电直导线中的电流的大小成正比,可以用公式B=k$\frac{I}{r}$来表示,其中k为比例常数,俯视图如图所示,在光滑水平面上有一通电直导线ab,旁边有一矩形金属线框cdef,cd边与导线ab平行,当导线ab中通如图所示电流时(设a流向b为电流的正方向),为使矩形金属线框cdef静止不动,需加一水平方向的力F(设向右为正方向),则正确的是( )



 现在高速公路上的标志牌都用“回归反光膜”制成,夜间行车时,它能把车灯射出的光逆向返回,标志牌上的字特别醒目.这种“回归反光膜”是用球体反射元件制成的,反光膜内均匀分布着直径为10μm的细玻璃珠,一束与主光轴MN平行的入射光经玻璃珠折射→反射→再折射后恰好和入射光平行,如图所示.
现在高速公路上的标志牌都用“回归反光膜”制成,夜间行车时,它能把车灯射出的光逆向返回,标志牌上的字特别醒目.这种“回归反光膜”是用球体反射元件制成的,反光膜内均匀分布着直径为10μm的细玻璃珠,一束与主光轴MN平行的入射光经玻璃珠折射→反射→再折射后恰好和入射光平行,如图所示. 如图所示的竖直平面内,相距为d不带电且足够大的平行金属板M、N水平固定放置,与灯泡L、开关S组成回路并接地,M板上方有一带电微粒发射源盒D,灯泡L的额定功率与电压分别为PL、UL.电荷量为q、质量为m1的带电微粒以水平向右的速度v0从D盒右端口距M板h高处连续发射,落在M板上其电荷立即被吸收且在板面均匀分布,板间形成匀强电场,当M板吸收一定电量后闭合开关S,灯泡能维持正常发光,质量为m2的带电粒子Q以水平速度从左侧某点进入板间,并保持该速度穿过M、N板.设带电微粒可视为质点,重力加速度为g,忽略带电微粒间的相互作用及空气阻力,试分析下列问题:
如图所示的竖直平面内,相距为d不带电且足够大的平行金属板M、N水平固定放置,与灯泡L、开关S组成回路并接地,M板上方有一带电微粒发射源盒D,灯泡L的额定功率与电压分别为PL、UL.电荷量为q、质量为m1的带电微粒以水平向右的速度v0从D盒右端口距M板h高处连续发射,落在M板上其电荷立即被吸收且在板面均匀分布,板间形成匀强电场,当M板吸收一定电量后闭合开关S,灯泡能维持正常发光,质量为m2的带电粒子Q以水平速度从左侧某点进入板间,并保持该速度穿过M、N板.设带电微粒可视为质点,重力加速度为g,忽略带电微粒间的相互作用及空气阻力,试分析下列问题: