题目内容
11.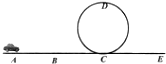 低碳环保绿色出行的理念逐渐深入人心,而纯电动汽车是时下相对较环保的汽车,为宣传“低碳环保”健康生活理念,某次志愿者举行玩具电动小汽车的表演,如图所示,质量m=2kg的小汽车以vo=4m/s的初速度从水平轨迹A处出发,沿平直轨道AC运动,到达C点时关闭发动机,进入半径R=1.8m圆轨道,恰能做完整的圆周运动后又进入CE水平轨道向右运动,直至停下,已知小汽车与水平面的摩擦阻力恒为重力的0.1倍,AB段运动过程中风力较大,可能化为受0.8N的水平向左的作用力,过B点后小汽车所受空气作用力均忽略不计,圆轨道可视作光滑,已知AB段长度x1=3m,BC段长度x2=2m,CE段足够长,小汽车自身长度可忽略,求:
低碳环保绿色出行的理念逐渐深入人心,而纯电动汽车是时下相对较环保的汽车,为宣传“低碳环保”健康生活理念,某次志愿者举行玩具电动小汽车的表演,如图所示,质量m=2kg的小汽车以vo=4m/s的初速度从水平轨迹A处出发,沿平直轨道AC运动,到达C点时关闭发动机,进入半径R=1.8m圆轨道,恰能做完整的圆周运动后又进入CE水平轨道向右运动,直至停下,已知小汽车与水平面的摩擦阻力恒为重力的0.1倍,AB段运动过程中风力较大,可能化为受0.8N的水平向左的作用力,过B点后小汽车所受空气作用力均忽略不计,圆轨道可视作光滑,已知AB段长度x1=3m,BC段长度x2=2m,CE段足够长,小汽车自身长度可忽略,求:(1)要使小汽车完成上述运动,AC段电动机至少提供多少能量?
(2)若CE阶段启用动力回收系统,把机械能转化为电能,回收效率为30%,则该段小汽车还能滑行多远?
分析 (1)要使小汽车恰好完成上述运动时,通过最高点D点时由重力提供向心力,由牛顿第二定律求出D点的临界速度.再对AD段过程,运用动能定理列式求解.
(2)对DC段运用动能定理,求出小汽车通过C点的速度,再由能量守恒定律求解.
解答 解:(1)小汽车与水平轨道间的摩擦阻力 f=0.1mg,
代入数据得:f=2N
设小车通过D点的速度为v1,如果小车恰能做完整的圆周运动,在D点应有:
mg=m$\frac{{v}_{1}^{2}}{R}$
从A到D的过程,运用动能定理有:
W-f(x1+x2)-Fx1-2mgR=$\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}m{v}_{0}^{2}$
解得电动机至少做功为:W=86.4J
(2)从D到C的过程,运用动能定理有:
2mgR=$\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}$
代入数据解得:v2=3$\sqrt{10}$m/s
若在CE阶段开启动力回收系统,回收效率为 30%,即有70%的能量用于克服摩擦力做功,即有:
-fx3=0-$\frac{1}{2}m{v}_{2}^{2}$×70%
滴入数据解得:x3=31.5m
则该段小汽车还能滑行31.5m.
答:(1)要使小汽车完成上述运动,AC段电动机至少提供86.4J的能量.
(2)该段小汽车还能滑行31.5m.
点评 解决本题的关键一要把握圆周运动的临界条件:最高点由重力充当向心力.二是正确分析能量是如何转化的,运用能量守恒定律研究能量问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图所示,跨过光滑定滑轮的细线两端连着a、b两个小球,a、b的质量分别为m、M(且m<M),细线、滑轮的质量不计,忽略空气的阻力,重力加速度为g,先用手摁住a,然后由静止释放两物体(细线足够长),在b落地前,细线的拉力为( )
如图所示,跨过光滑定滑轮的细线两端连着a、b两个小球,a、b的质量分别为m、M(且m<M),细线、滑轮的质量不计,忽略空气的阻力,重力加速度为g,先用手摁住a,然后由静止释放两物体(细线足够长),在b落地前,细线的拉力为( )
 如图所示,跨过光滑定滑轮的细线两端连着a、b两个小球,a、b的质量分别为m、M(且m<M),细线、滑轮的质量不计,忽略空气的阻力,重力加速度为g,先用手摁住a,然后由静止释放两物体(细线足够长),在b落地前,细线的拉力为( )
如图所示,跨过光滑定滑轮的细线两端连着a、b两个小球,a、b的质量分别为m、M(且m<M),细线、滑轮的质量不计,忽略空气的阻力,重力加速度为g,先用手摁住a,然后由静止释放两物体(细线足够长),在b落地前,细线的拉力为( )| A. | $\frac{{{m^2}g}}{M+m}$ | B. | $\frac{{{M^2}g}}{M+m}$ | C. | $\frac{2Mmg}{M+m}$ | D. | $\frac{M-m}{M+m}Mg$ |
16. 如图所示,在水平向右的匀强电场中有一绝缘的斜面,斜面上的带电物块沿斜面滑下,已知在下滑过程中,金属块动能增加了10J,金属块克服摩擦力做功6J,重力做功18J,下列判断中正确的是( )
如图所示,在水平向右的匀强电场中有一绝缘的斜面,斜面上的带电物块沿斜面滑下,已知在下滑过程中,金属块动能增加了10J,金属块克服摩擦力做功6J,重力做功18J,下列判断中正确的是( )
 如图所示,在水平向右的匀强电场中有一绝缘的斜面,斜面上的带电物块沿斜面滑下,已知在下滑过程中,金属块动能增加了10J,金属块克服摩擦力做功6J,重力做功18J,下列判断中正确的是( )
如图所示,在水平向右的匀强电场中有一绝缘的斜面,斜面上的带电物块沿斜面滑下,已知在下滑过程中,金属块动能增加了10J,金属块克服摩擦力做功6J,重力做功18J,下列判断中正确的是( )| A. | 金属块带正电 | B. | 金属块的机械能减少8J | ||
| C. | 金属块克服电场力做功2J | D. | 金厲块的电势能减少2J |
3. 如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为mA和mB,由于B球受到水平风力作用,A与B球一起向右匀速运动,已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )
如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为mA和mB,由于B球受到水平风力作用,A与B球一起向右匀速运动,已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )
 如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为mA和mB,由于B球受到水平风力作用,A与B球一起向右匀速运动,已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )
如图所示,水平细杆上套一环A,环A与球B间用一不可伸长轻质绳相连,质量分别为mA和mB,由于B球受到水平风力作用,A与B球一起向右匀速运动,已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )| A. | A球受到3个力 | |
| B. | B球受到的风力大小为mBgtanθ | |
| C. | 杆对A球的支持力随着风力的增加而增加 | |
| D. | 当风力增大时,A受到的摩擦力也将增大 |
20. 如图是一种延时继电器的示意图,铁芯上有两个金属线圈A和B,线圈A与电源E相连,线圈B两端连在一起,构成一个闭合电路.将开关S断开,弹簧过一会儿才会将衔铁D拉起使工作电路断开.则下列说法中不正确的是( )
如图是一种延时继电器的示意图,铁芯上有两个金属线圈A和B,线圈A与电源E相连,线圈B两端连在一起,构成一个闭合电路.将开关S断开,弹簧过一会儿才会将衔铁D拉起使工作电路断开.则下列说法中不正确的是( )
 如图是一种延时继电器的示意图,铁芯上有两个金属线圈A和B,线圈A与电源E相连,线圈B两端连在一起,构成一个闭合电路.将开关S断开,弹簧过一会儿才会将衔铁D拉起使工作电路断开.则下列说法中不正确的是( )
如图是一种延时继电器的示意图,铁芯上有两个金属线圈A和B,线圈A与电源E相连,线圈B两端连在一起,构成一个闭合电路.将开关S断开,弹簧过一会儿才会将衔铁D拉起使工作电路断开.则下列说法中不正确的是( )| A. | 电源电动势越大,则从断开S到断开工作电路的时间间隔越短 | |
| B. | 线圈B的匝数越多,则从断开S到断开工作电路的时间间隔越长 | |
| C. | 在断开S瞬间,线圈B中有感应电流产生 | |
| D. | 若将线圈B的两端断开,则在断开S瞬间,线圈B两端一定产生感应电动势 |
1.关于曲线运动的说法中正确的是( )
| A. | 速度变化的运动必定是曲线运动 | |
| B. | 做曲线运动的物体加速度方向跟它的速度方向不在同一直线上 | |
| C. | 受恒力作用的物体可能做曲线运动 | |
| D. | 加速度变化的运动必定是曲线运动 |
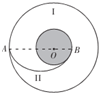 开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.该定律对一切具有中心天体的引力系统都成立.如图,嫦娥三号探月卫星在半径为r的圆形轨道I上绕月球运行,周期为T.月球的半径为R,引力常量为G.某时刻嫦娥三号卫星在4点变轨进入椭圆轨道II,在月球表面的B点着陆.A、O、B三点在一条直线上.
开普勒第三定律指出:所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.该定律对一切具有中心天体的引力系统都成立.如图,嫦娥三号探月卫星在半径为r的圆形轨道I上绕月球运行,周期为T.月球的半径为R,引力常量为G.某时刻嫦娥三号卫星在4点变轨进入椭圆轨道II,在月球表面的B点着陆.A、O、B三点在一条直线上.
