题目内容
19. 某仓库中常用的皮带传输装置由两台皮带传送机组成,一台水平传送,A、B两端相距4m,另一台倾斜,传送带的倾角θ=37°,C、D两端相距4.2m,B、C相距很近.水平部分AB以5m/s的速率顺时针转动,将质量为20kg的一袋大米无初速度地放在A端,到达B端后,速度大小不变地传到倾斜送带的CD部分,米袋与传送带AB间的动摩擦因数为0.2,米袋与传送带CD间的动摩擦因数为0.8.(g取10m/s2)试求:
某仓库中常用的皮带传输装置由两台皮带传送机组成,一台水平传送,A、B两端相距4m,另一台倾斜,传送带的倾角θ=37°,C、D两端相距4.2m,B、C相距很近.水平部分AB以5m/s的速率顺时针转动,将质量为20kg的一袋大米无初速度地放在A端,到达B端后,速度大小不变地传到倾斜送带的CD部分,米袋与传送带AB间的动摩擦因数为0.2,米袋与传送带CD间的动摩擦因数为0.8.(g取10m/s2)试求:(1)从A点运动到B点的过程中,米袋与传送带之间因摩擦产生的热量;
(2)CD部分传送带顺时针运转,若要米袋能以最短的时间从C端传送到D端,求CD运转的速度应满足的条件及米袋从C端传送到D端的最短时间.
分析 (1)根据牛顿运动定律求解加速度,根据运动学知识求解位移,从的相对位移,根据热量Q=f△x求热量;
(2)若CD部分传送带的速度较大,使米袋沿CD上滑时所受摩擦力一直沿皮带向上,则所用时间最短,根据匀变速直线运动规律解时间和速度.
解答 解:(1)米袋在传送带的滑动摩擦力作用下做匀加速直线运动,在水平方向开始只受滑动摩擦力故有:F合=f=μmg=ma1,
所以米袋的加速度为:a1=μ1g=2m/s2,
米袋在水平传送带上的最大速度为vmax=5m/s,所以其加速时间为t1=$\frac{{v}_{max}}{{a}_{1}}$=$\frac{5}{2}$=2.5s,
这过程中米袋的位移为:x1=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$=$\frac{1}{2}×2×2.{5}^{2}$=6.25m,
因为x1>L,说明米袋一直加速运动时间为t′=$\sqrt{\frac{2L}{{a}_{1}}}$=$\sqrt{\frac{2×4}{2}}$=2s,
米袋相对传送带的位移为△x=vt′-L=5×2-4=6m,
故产生热量Q=f△x=0.2×200×6=240J;
(2)若CD部分传送带的速度较大,使米袋沿CD上滑时所受摩擦力一直沿皮带向上,
则所用时间最短,此种情况米袋加速度一直为a2=g(-sinθ+μ2cosθ)=10(-0.6+0.8×0.8)=0.4m/s2
由SCD=v0tmin+$\frac{1}{2}$a2t2min,①
v0=a1t′②
①②联立解得:tmin=1s③
到达D点速度为vD=v0+a2tmin④
②③④解得vD=4.4m/s.
答:(1)从A点运动到B点的过程中,米袋与传送带之间因摩擦产生的热量为240J;
(2)CD部分传送带顺时针运转,若要米袋能以最短的时间从C端传送到D端,CD运转的速度应满足大于等于4.4m/s,米袋从C端传送到D端的最短时间为1s.
点评 本题难点在于通过分析题意找出临条界件,注意米袋在CD段所可能做的运动情况,从而分析得出使米袋沿CD上滑时所受摩擦力一直沿皮带向上,则所用时间最短;本题的难度较大

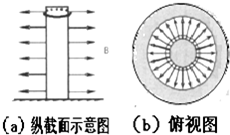 根据实际需要,磁铁可以制造成多种形状,如图就是一根很长的光滑圆柱形磁棒,在它的侧面有均匀向外的辐射状磁场.现将磁棒竖直固定在水平面上,磁棒外套有一个粗细均匀圆形金属线圈,金属线圈的质量为m,半径为R,电阻为r,金属线圈所在位置的磁场的磁感应强度为B.让金属线圈从磁棒上端静止释放,经一段时间后与水平面相碰并原速率反弹,又经时间t,上升速度减小到零.则关于金属线圈与地面撞击前的速度ν,撞击反弹后上升到最高点的过程中,通过金属线圈某一截面的电量q,下列说法中正确的是( )
根据实际需要,磁铁可以制造成多种形状,如图就是一根很长的光滑圆柱形磁棒,在它的侧面有均匀向外的辐射状磁场.现将磁棒竖直固定在水平面上,磁棒外套有一个粗细均匀圆形金属线圈,金属线圈的质量为m,半径为R,电阻为r,金属线圈所在位置的磁场的磁感应强度为B.让金属线圈从磁棒上端静止释放,经一段时间后与水平面相碰并原速率反弹,又经时间t,上升速度减小到零.则关于金属线圈与地面撞击前的速度ν,撞击反弹后上升到最高点的过程中,通过金属线圈某一截面的电量q,下列说法中正确的是( )| A. | $ν=\frac{mgr}{{4{B^2}{R^2}}}$ | B. | $q=\frac{mgt}{2BπR}$ | ||
| C. | $q=\frac{{{m^2}gr}}{{8{π^3}{B^3}{R^3}}}-\frac{mgt}{2πBR}$ | D. | q=0 |

①甲同学用多用表的直流电压挡,选择0~1V量程,直接测铜锌两金属片之间的电压时示数为0.82V;若已知该水果电池的内阻约为2100Ω,则该水果电池的电动势应大于(填“大于”“等于”或“小于”)0.82V.
②乙同学利用伏安法并借助DIS实验器材中的电压传感器、电流传感器测水果电池的电动势和内阻,电路如图乙所示.表是乙同学测量该水果电池时记录的数据.
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 电压U/A | 0.32 | 0.36 | 0.44 | 0.52 | 0.60 | 0.68 |
| 电流I/mA | 0.32 | 0.30 | 0.26 | 0.22 | 0.18 | 0.14 |
 如图所示为2014年索契冬奥会上中国女子冰壶队员投掷冰壶的镜头.在某次投掷中,冰壶运动一段时间后以0.4m/s的速度与对方的静止冰壶发生正碰,碰后对方的冰壶以0.3m/s的速度向前滑行.若两冰壶质量相等,规定向前运动方向为正方向,则碰后中国队冰壶获得的速度为( )
如图所示为2014年索契冬奥会上中国女子冰壶队员投掷冰壶的镜头.在某次投掷中,冰壶运动一段时间后以0.4m/s的速度与对方的静止冰壶发生正碰,碰后对方的冰壶以0.3m/s的速度向前滑行.若两冰壶质量相等,规定向前运动方向为正方向,则碰后中国队冰壶获得的速度为( )| A. | -0.1 m/s | B. | -0.7m/s | C. | 0.1 m/s | D. | 0.7m/s |
 重力大小为G的小物块,静止在球形碗内的图示位置.物块受到的支持力大小为N,摩擦力大小为f,则( )
重力大小为G的小物块,静止在球形碗内的图示位置.物块受到的支持力大小为N,摩擦力大小为f,则( )| A. | G=N+f | B. | G=N | C. | G<f | D. | G>f |
 由粗糙的水平杆AO与光滑的竖直杆BO组成的绝缘直角支架如图放置,在AO杆、BO杆上套有带正电的小球P、Q,两个小球恰能在某一位置平衡.现将P缓慢地向左移动一小段距离,两球再次达到平衡.若小球所带电量不变,与移动前相比( )
由粗糙的水平杆AO与光滑的竖直杆BO组成的绝缘直角支架如图放置,在AO杆、BO杆上套有带正电的小球P、Q,两个小球恰能在某一位置平衡.现将P缓慢地向左移动一小段距离,两球再次达到平衡.若小球所带电量不变,与移动前相比( )| A. | P、Q之间的距离增大 | B. | 杆BO对Q的弹力减小 | ||
| C. | 杆AO对P的摩擦力增大 | D. | 杆AO对P的弹力减小 |
 如图甲所示是用来测量重力加速度的装置,试验时通过电磁铁控制小铁球从A处自由下落,小铁球下落过程中依次经过并遮挡两个光电门B、C,B、C光电门测得光束被遮挡的时间分别为t1、t2,用刻度尺测量出B、C光电门的高差h.
如图甲所示是用来测量重力加速度的装置,试验时通过电磁铁控制小铁球从A处自由下落,小铁球下落过程中依次经过并遮挡两个光电门B、C,B、C光电门测得光束被遮挡的时间分别为t1、t2,用刻度尺测量出B、C光电门的高差h.