题目内容
6.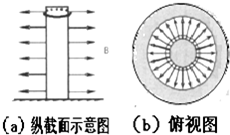 根据实际需要,磁铁可以制造成多种形状,如图就是一根很长的光滑圆柱形磁棒,在它的侧面有均匀向外的辐射状磁场.现将磁棒竖直固定在水平面上,磁棒外套有一个粗细均匀圆形金属线圈,金属线圈的质量为m,半径为R,电阻为r,金属线圈所在位置的磁场的磁感应强度为B.让金属线圈从磁棒上端静止释放,经一段时间后与水平面相碰并原速率反弹,又经时间t,上升速度减小到零.则关于金属线圈与地面撞击前的速度ν,撞击反弹后上升到最高点的过程中,通过金属线圈某一截面的电量q,下列说法中正确的是( )
根据实际需要,磁铁可以制造成多种形状,如图就是一根很长的光滑圆柱形磁棒,在它的侧面有均匀向外的辐射状磁场.现将磁棒竖直固定在水平面上,磁棒外套有一个粗细均匀圆形金属线圈,金属线圈的质量为m,半径为R,电阻为r,金属线圈所在位置的磁场的磁感应强度为B.让金属线圈从磁棒上端静止释放,经一段时间后与水平面相碰并原速率反弹,又经时间t,上升速度减小到零.则关于金属线圈与地面撞击前的速度ν,撞击反弹后上升到最高点的过程中,通过金属线圈某一截面的电量q,下列说法中正确的是( )| A. | $ν=\frac{mgr}{{4{B^2}{R^2}}}$ | B. | $q=\frac{mgt}{2BπR}$ | ||
| C. | $q=\frac{{{m^2}gr}}{{8{π^3}{B^3}{R^3}}}-\frac{mgt}{2πBR}$ | D. | q=0 |
分析 (1)线圈下落过程中垂直切割磁感线,产生感应电动势,由E=BLv、I=$\frac{E}{r}$、FA=BIL得到安培力的表达式,由牛顿第二定律分析线圈加速度的变化,判断线圈的运动情况:安培力逐渐增大,加速度逐渐减小,当安培力与重力平衡时,线圈做匀速直线运动,速度达到最大,由平衡条件可求出最大速度.
(2)根据牛顿第二定律得到反弹上升过程中线圈加速度的表达式,采用积分法求出电量q
解答 解:A、线圈第一次下落过程中有E=B•2πRv、I=$\frac{E}{r}$、FA=BIL=BI•2πR,得安培力大小为:
FA=$\frac{4{π}^{2}{B}^{2}{R}^{2}v}{r}$
根据牛顿第二定律得:
mg-FA=ma
可知线圈做加速度减小的加速运动,当a=0时,速度最大,代入求得最大速度为:υm=$\frac{mgr}{4{π}^{2}{B}^{2}{R}^{2}}$,故A错误;
B、反弹后上升的过程中某一时刻,由牛顿运动定律得:mg+BI•2πR=ma
则得:mg△t+BI•2πR•△t=ma△t
在一段微小时间△t内,速度增量为△υ=a△t,通过线圈截面电量为:△q=I△t
则:△q=$\frac{ma△t-mg△t}{2πBR}$
得到:∑△q=$\frac{∑(ma-mg)△t}{2πBR}$,
又∑ma△t=∑m△v=mvm=$\frac{{m}^{2}gr}{4{π}^{2}{B}^{2}{R}^{2}}$,
∑mg△t=mgt1,
故:q=$\frac{{m}^{2}gr}{8{π}^{3}{B}^{3}{R}^{3}}$-$\frac{mg{t}_{1}}{2πBR}$,故C正确,BD错误;
故选:C.
点评 本题是电磁感应问题,难点是采用积分法求解非匀变速运动的速度和高度,从牛顿第二定律入手,采取微元法,得到一段微小时间△t内速度的变化量和高度变化量,再积分.难度较大,考查运用数学知识处理物理问题的能力.

 高中必刷题系列答案
高中必刷题系列答案 如图所示,在滑动变阻器的滑片向左滑动的过程中,理想电压表、电流表的示数将发生变化,电压表V1、V2示数变化量的绝对值分别为△U1、△U2,已知电阻R大于电源内阻r,则( )
如图所示,在滑动变阻器的滑片向左滑动的过程中,理想电压表、电流表的示数将发生变化,电压表V1、V2示数变化量的绝对值分别为△U1、△U2,已知电阻R大于电源内阻r,则( )| A. | 电流表A的示数增大 | B. | 电压表V2的示数增大 | ||
| C. | 电压表V1的示数增大 | D. | △U1大于△U2 |
 如图所示,在距离地面H高处的空中将小球以某一初速度水平向右抛出后,球撞击到竖直挡板上,结果落在抛出点正下方左侧S处,若将竖直挡板右移x,让球仍从原位置以相同的初速度水平抛出撞击到竖直挡板上,结果落在抛出点正下方右侧S处,若球以垂直于挡板的速度撞击时等速率反弹,则下列说法正确的是( )
如图所示,在距离地面H高处的空中将小球以某一初速度水平向右抛出后,球撞击到竖直挡板上,结果落在抛出点正下方左侧S处,若将竖直挡板右移x,让球仍从原位置以相同的初速度水平抛出撞击到竖直挡板上,结果落在抛出点正下方右侧S处,若球以垂直于挡板的速度撞击时等速率反弹,则下列说法正确的是( )| A. | x=2S | |
| B. | 不加挡板时球的落地点在抛出点正下方右侧3S处 | |
| C. | 两次小球抛出的初速度为2S$\sqrt{\frac{g}{2H}}$ | |
| D. | 小球两次撞击挡板位置的高度差为$\frac{3H}{5}$ |
| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫科学假说法 | |
| B. | 在探究金属丝电阻率与金属丝长度、横截面等关系时,应用了控制变量法 | |
| C. | 根据速度定义式v=$\frac{△x}{△t}$,当△t趋近于零时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,应用了等效替代的方法 | |
| D. | 卡文迪许扭秤实验测万有引力常量时,主要用到类比的方法 |
 传送带与水平面夹角为θ=37°,传送带以10m/s的速率沿顺时针方向转动,今在传送带上端A处无初速度地放上一个质量为1kg的小煤块(可视为质点),它与传送带间的动摩擦因数为0.5,若传送带A到B的长度为16m,g取10m/s2,则小煤块从A运动到B的过程中( )(sin37°=0.6,cos37°=0.8)
传送带与水平面夹角为θ=37°,传送带以10m/s的速率沿顺时针方向转动,今在传送带上端A处无初速度地放上一个质量为1kg的小煤块(可视为质点),它与传送带间的动摩擦因数为0.5,若传送带A到B的长度为16m,g取10m/s2,则小煤块从A运动到B的过程中( )(sin37°=0.6,cos37°=0.8)| A. | 小煤块从A运动到B的时间为2s | |
| B. | 煤块对皮带做的功为0 | |
| C. | 小煤块在白色皮带上留下黑色印记的长度为6m | |
| D. | 因煤块和皮带之间的摩擦而产生的内能为24J |
| A. | 椭圆轨道的一个焦点与地心重合 | |
| B. | 卫星与地心的连线在相等时间内扫过的面积相等 | |
| C. | 卫星的线速度在不断变化,与地心距离越大线速度越小 | |
| D. | 卫星的角速度在不断变化,与地心距离越大角速度越大 |
 如图所示,B是一个螺线管,C是与螺线管相连接的金属线圈.在B的正上方用绝缘丝线悬挂一个金属圆环A,A的环面水平且与螺线管的横截面平行.若仅在金属线圈C所处的空间加上与C环面垂直的变化磁场,发现在t1至t2时间段内绝缘丝线的拉力变小,则金属线圈C处所加磁场的磁感应强度随时间变化的B-t图象可能是( )
如图所示,B是一个螺线管,C是与螺线管相连接的金属线圈.在B的正上方用绝缘丝线悬挂一个金属圆环A,A的环面水平且与螺线管的横截面平行.若仅在金属线圈C所处的空间加上与C环面垂直的变化磁场,发现在t1至t2时间段内绝缘丝线的拉力变小,则金属线圈C处所加磁场的磁感应强度随时间变化的B-t图象可能是( )




 某仓库中常用的皮带传输装置由两台皮带传送机组成,一台水平传送,A、B两端相距4m,另一台倾斜,传送带的倾角θ=37°,C、D两端相距4.2m,B、C相距很近.水平部分AB以5m/s的速率顺时针转动,将质量为20kg的一袋大米无初速度地放在A端,到达B端后,速度大小不变地传到倾斜送带的CD部分,米袋与传送带AB间的动摩擦因数为0.2,米袋与传送带CD间的动摩擦因数为0.8.(g取10m/s2)试求:
某仓库中常用的皮带传输装置由两台皮带传送机组成,一台水平传送,A、B两端相距4m,另一台倾斜,传送带的倾角θ=37°,C、D两端相距4.2m,B、C相距很近.水平部分AB以5m/s的速率顺时针转动,将质量为20kg的一袋大米无初速度地放在A端,到达B端后,速度大小不变地传到倾斜送带的CD部分,米袋与传送带AB间的动摩擦因数为0.2,米袋与传送带CD间的动摩擦因数为0.8.(g取10m/s2)试求: