题目内容
5.为了探寻暗物质存在的证据,我国于2015年12月17日发射了一颗被命名为“悟空”的暗物质粒子探测卫星,卫星成功进入500千米预定轨道.已知地球的半径为6400千米,同步卫星的高度为36000千米,则下列判断正确的是( )| A. | “悟空”的运行周期大于地球自转的周期 | |
| B. | “悟空”的向心加速度小于地球表面的重力加速度 | |
| C. | “悟空”的运行线速度大于地球的第一宇宙速度 | |
| D. | “悟空”的向心加速度小于地球赤道上的物体随地球自转的向心加速度 |
分析 已知“悟空”做匀速圆周运动的轨道半径为r,由万有引力提供向心力即可求出运动周期T,线速度v,向心加速度a的公式.
解答 解:A、由万有引力提供向心力得:$\frac{GMm}{(R+{h}_{1})^{2}}=\frac{m•4{π}^{2}(R+{h}_{1})}{{T}_{1}^{2}}$
对同步卫星:$\frac{GMm′}{{(R+{h}_{2})}^{2}}=\frac{m•4{π}^{2}(R+{h}_{2})}{{T}_{同}^{2}}$
由于同步卫星的轨道大于“悟空”的轨道,所以同步卫星的周期大于“悟空”的周期,而同步卫星的周期与地球的自转周期是相等的,所以“悟空”的运行周期小于地球自转的周期.故A错误;
B、“悟空”受到的向心力:ma=$\frac{GMm}{{(R+{h}_{1})}^{2}}$$<\frac{GMm}{{R}^{2}}$=mg,所以可知“悟空”的向心加速度小于地球表面的重力加速度.故B正确;
C、根据万有引力提供向心力得:$\frac{GMm}{{(R+{h}_{1})}^{2}}=\frac{m{v}^{2}}{(R+{h}_{1})}$,而物体的第一宇宙速度满足$\frac{GMm}{{R}^{2}}=\frac{m{v}_{1}^{2}}{{R}^{2}}$,可知“悟空”的运行线速度小于地球的第一宇宙速度.故C 错误;
D、“悟空”的运行周期小于地球自转的周期,则“悟空”的运行角速度大于地球自转的角速度;又由于“悟空”的轨道半径大于地球的半径,由:a=ω2r可知,“悟空”的向心加速度一定大于地球赤道上的物体随地球自转的向心加速度.故D错误.
故选:B
点评 本题的关键抓住万有引力提供向心力,列式求解出线速度、周期、向心加速度的表达式是解答的前提条件.

| A. | x=vt+$\frac{1}{2}$at2 | B. | x=-vt+$\frac{1}{2}$at2 | C. | x=-vt-$\frac{1}{2}$at2 | D. | x=vt-$\frac{1}{2}$at2 |
| A. | 物体发生形变时,其重心位置一定不变 | |
| B. | 物体升高时,只要物体的形状和质量分布情况不变,其重心在空中位置一定不变 | |
| C. | 将物体悬挂起来平衡时,重心必在悬挂点的正下方 | |
| D. | 形状规则的物体重心必在其几何中心处 |
 如图,ACB为光滑固定的半圆形轨道,A、B为水平直径的两个端点,AC为四分之一圆弧,MPQO为有界的竖直向下的匀强电场,其他区域均无电场.一个带负电的小球,从A点正上方高为H处由静止释放,然后进入半圆轨道,不计空气阻力,关于小球的运动,下列说法正确的是( )
如图,ACB为光滑固定的半圆形轨道,A、B为水平直径的两个端点,AC为四分之一圆弧,MPQO为有界的竖直向下的匀强电场,其他区域均无电场.一个带负电的小球,从A点正上方高为H处由静止释放,然后进入半圆轨道,不计空气阻力,关于小球的运动,下列说法正确的是( )| A. | 小球在AC部分可能做匀速圆周运动 | |
| B. | 小球一定能从B点离开轨道 | |
| C. | 若小球能从B点离开,上升的高度一定小于H | |
| D. | 小球到达C点的速度可能为零 |
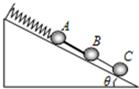 如图所示,A、B、C三球质量均为m,轻质弹簧一端固定在斜面顶端、另一端与A球相连,A、B间固定一个轻杆,B、C间由一轻质细线连接.倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )
如图所示,A、B、C三球质量均为m,轻质弹簧一端固定在斜面顶端、另一端与A球相连,A、B间固定一个轻杆,B、C间由一轻质细线连接.倾角为θ的光滑斜面固定在地面上,弹簧、轻杆与细线均平行于斜面,初始系统处于静止状态,细线被烧断的瞬间,已知重力加速度为g,下列说法正确的是( )| A. | A球的受力情况未变,加速度为零 | |
| B. | C球的加速度沿斜面向下,大小为$\frac{g}{2}$ | |
| C. | A、B之间杆的拉力大小为2mgsinθ | |
| D. | A、B两个小球的加速度均沿斜面向上,大小均为$\frac{1}{2}$gsinθ |

| A. | 弹簧测力计的示数是30N | |
| B. | 弹簧测力计的示数是18N | |
| C. | 在突然撤去F的瞬间,弹簧测力计的示数为零 | |
| D. | 在突然撤去F的瞬间,m1的加速度9m/s2 |
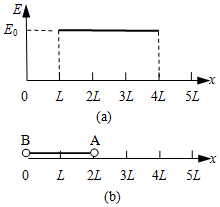 光滑绝缘水平面上有一水平向右的匀强电场,其场强大小分布如图(a)所示.两个质量均为m的带电小球A和B由长为2L的轻杆相连,组成一带电系统,球A带电量为+2q,球B带电量为-q.t=0时刻,带电系统由如图(b)所示位置从静止开始运动.若视小球为质点,不计轻杆的质量,求:
光滑绝缘水平面上有一水平向右的匀强电场,其场强大小分布如图(a)所示.两个质量均为m的带电小球A和B由长为2L的轻杆相连,组成一带电系统,球A带电量为+2q,球B带电量为-q.t=0时刻,带电系统由如图(b)所示位置从静止开始运动.若视小球为质点,不计轻杆的质量,求: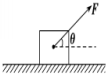 质量为m=2kg的物体,静止放在水平面上,它们之间的动摩擦因数μ=0.5,现对物体施加F=20N的作用力,方向与水平面成θ=37°角斜向上,如图所示,(sin 37°=0.6,cos37°=0.80,g取10m/s2)求:
质量为m=2kg的物体,静止放在水平面上,它们之间的动摩擦因数μ=0.5,现对物体施加F=20N的作用力,方向与水平面成θ=37°角斜向上,如图所示,(sin 37°=0.6,cos37°=0.80,g取10m/s2)求: